Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?


Dựa vào giản đồ xét tam giác vuông OAB có
\(\sin60=\frac{Uc}{U_{ }AB}\Rightarrow U_C=100.\sin60=50\sqrt{3}V\Rightarrow Z_C=\frac{U_C}{I}=\frac{50\sqrt{3}}{0.5}=100\sqrt{3}\Omega\)
=> \(C=\frac{1}{Z_C.\omega}\)
\(\cos60=\frac{U_R}{U_{AB}}\Rightarrow U_R=50\Omega\Rightarrow R=\frac{U_R}{I}=100\Omega\)
2. Công suất trên mạch có biểu thức
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\\=\frac{U^2}{R^{ }+\frac{\left(Z_L-Z_C\right)^2}{R}}\)
L thay đổi để P max <=> Mẫu Min => áp dụng bất đẳng thức cô-si cho hai số không âm=> \(R=\left|Z_L-Z_C\right|\)
=> \(R=100-40=60\Omega\)
=>

Đáp án D
+ Cảm kháng của tụ điện Z L = L ω = 120 Ω
Hai giá trị của R cho cùng công suất
![]()

Chọn đáp án D
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P.
Ta luôn có
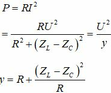
Theo bất đẳng thức Cosi ta có:
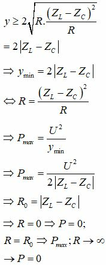
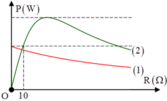
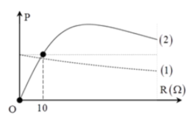
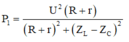
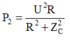
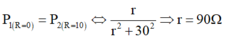

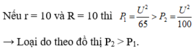



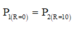
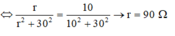
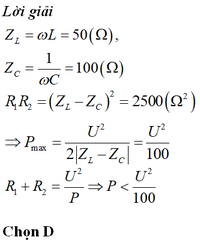
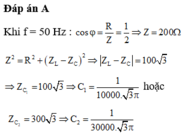

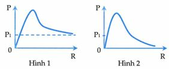
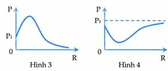
Ta có P 1 = U 2 R + r R + r 2 + Z L − Z C 2
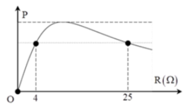
Dạng đồ thị cho thấy rằng r > Z L − Z C = 30 Ω
P 1 = U 2 R R 2 + Z C 2
P 1 R = 0 = P 2 R = 10 ⇔ r r 2 + 30 2 = 10 10 2 + 30 2 ⇒ r = 90 Ω
Đáp án D