Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
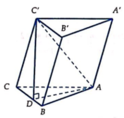
Theo giả thiết ta có CD' ⊥ (ABC). Áp dụng định lý Cô-sin cho ∆ ABD ta được:
AD = ![]()
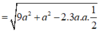
![]()
Hình chiếu vuông góc của AC’ trên mặt phẳng (ABC) là AD, vì vậy ta có góc giữa AC' và mặt phẳng (ABC) là góc C ' A D ^ = 45 0 => ∆ C'AD vuông cân tại D
![]()
Diện tích
∆
ABC là 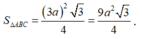
Do đó 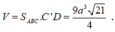

Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AA'}=\overrightarrow{c}\)
với \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\)
và \(\left|\overrightarrow{a}\right|=a,\overrightarrow{\left|b\right|}=a\sqrt{2},\left|\overrightarrow{c}\right|=a\sqrt{3}\)
khi đó
\(\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{c,}\overrightarrow{BC}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Giả sử đường vuông góc chung cắt \(\overrightarrow{AB}\) tại M và cắt \(\overrightarrow{BC'}\) tại N và \(\overrightarrow{AM}=x.\overrightarrow{AB'}=x.\overrightarrow{a}+x.\overrightarrow{c},\overrightarrow{BN}=y.\overrightarrow{BC'}=-y.\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Suy ra \(\overrightarrow{AN}=\left(1-y\right)\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Và do đó
\(\overrightarrow{MN}=\left(1-x-y\right)\overrightarrow{a}+y.\overrightarrow{b}+\left(y-x\right)\overrightarrow{c}\)
Ta có :
\(MN\perp AB',BC'\Leftrightarrow\begin{cases}\overrightarrow{MN}.\overrightarrow{AB}=0\\\overrightarrow{MN}.\overrightarrow{BC'}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-4x+2y+1=0\\-2x+6y-1=0\end{cases}\)
Giải hệ ta thu được \(x=\frac{2}{5},y=\frac{3}{10}\)
Từ đó :
\(MN^2=\left[\left(1-x-y\right)^2+2y^2+3\left(y-x\right)^2\right].a^2=\frac{39^a}{100}\)
Suy ra \(d\left(AB';BC'\right)=\frac{a\sqrt{39}}{10}\)


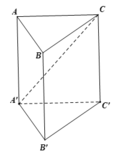
a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)

Đáp án A.
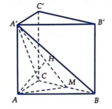
Gọi M là trung điểm của BC thì BC ⊥ (A'AM)
Từ A kẻ AH
⊥
A'M, ![]()
Suy ra
![]()
Góc giữa đường thẳng A'B và mặt phẳng (ABC) bằng góc A ' M A ^
Theo giả thiết ta có A ' M A ^ = 60 0
Đặt AB = 2x ![]()
Từ giả thiết ta có
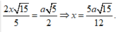
Do đó:
![]()
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính đúng như trên nhưng nhớ nhầm công thức tính thể tích khối lăng trụ sang công thức tính thể tích khối chớp.
Cụ thể
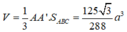
Phương án C: Sai do HS giải như trên và tìm được ![]() nhưng lại tính sai diện tích tam giác ABC. Cụ thể
nhưng lại tính sai diện tích tam giác ABC. Cụ thể
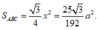
Do đó tính được
![]()
Phương án D: Sai do HS tính đúng như trên nhưng tính sai diện tích tam giác ABC. Cụ thể:
![]()
Do đó tính được V = 125 3 48 a 3

Đáp án D.
Gọi M là trung điểm BC, dựng ![]()
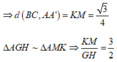
![]()
∆ AA'G vuông tại G, GH là đường cao => A'G = 1 3
Vậy 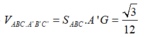

Đáp án C
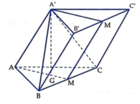
Ta dễ dàng chứng minh được AA'//(BCC'B')
![]()
![]()
Gọi G là trọng tâm của tam giác ABC. Suy ra A'G ⊥ (ABC)
Ta có
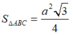
![]()
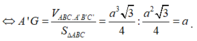
Lại có
![]()
![]()
Ta luôn có
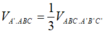
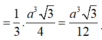
![]()
![]()

Gọi M, M' lần lượt là trung điểm của BC và B'C'. Ta có ![]() .
.![]()
Mà MM'//BB' nên BC ⊥ BB' => BCC'B' là hình chữ nhật
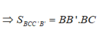
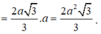
Từ:
![]()
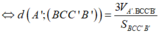
![]()
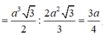
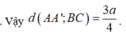


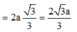
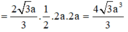

Đáp án A