Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

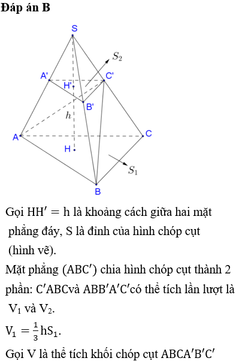
Đáp án B
Gọi HH' = h là khoảng cách giữa hai mặt phẳng đáy, S là đỉnh của hình chóp cụt (hình vẽ).
Mặt phẳng (ABC′) chia hình chóp cụt thành 2 phần: C′ABC và ABB′A′C′ có thể tích lần lượt là V 1 và V 2 .
V 1 = 1 3 h S
Gọi V là thể tích khối chóp cụt ABCA′B′C′
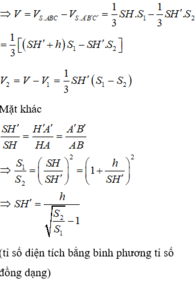
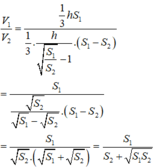

Đáp án C
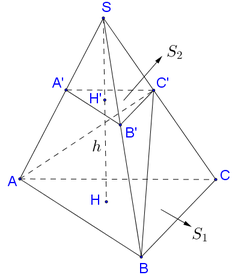
Ta có
B C ⊥ A C , B C ⊥ A A ' ⇒ B C ⊥ A ' A C C ' ⇒ B C ⊥ A ' C .
Suy ra
A ' C B , A B C ^ = A ' C , A C ^ = A ' C A ^ = x , 0 < x < π 2 .
Δ A ' A C vuông tại B nên
A A ' = A ' C . sin A ' C A ^ = a sin x ; A C = a cos x .
Suy ra
V A ' . A B C = 1 3 . A A ' . S Δ A B C = 1 3 . a sin x . a cos x 2 2 = a 3 6 sin x cos 2 x .
Xét hàm số
f x = sin x cos 2 x = sin x 1 − sin 2 x trên 0 ; π 2 .
Đặt t = sin x , do x ∈ 0 ; π 2 ⇒ t ∈ 0 ; 1 . Xét hàm số g t = t 1 − t 2 trên 0 ; 1 .
Ta có
f ' t = 1 − 3 t 2 ; f ' t = 0 ⇔ t = ± 1 3 .
Do t ∈ 0 ; 1 nên t = 1 3 .
Lập bảng biến thiên, suy ra max x ∈ 0 ; π 2 f x = max t ∈ 0 ; 1 g t = g 1 3 = 2 3 9 .
Vậy V max = a 3 6 . 2 3 9 = a 3 3 27 (đvtt).

1. Một khu đồi trồng cây ăn quả có tất cả 1950 cây, gồm các loại cam, quýt và vải thiều. Biết \(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều. Tính xem mỗi loại có bao nhiêu cây.
\(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây \(\Rightarrow\) \(\dfrac{6}{9}\) số cây cam bằng \(\dfrac{6}{10}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều
Ta có sơ đồ:
Cam |-------|-------|-------|-------|-------|-------|-------|-------|-------| (9 phần)
Quýt |-------|-------|-------|-------|-------|-------|-------|-------|-------|-------| (10 phần)
Vải |-------|-------|-------|-------|-------|-------|-------| (7 phần)
Số cây cam là:
\(1950:\left(9+10+7\right).9=675\) (cây)
Số cây quýt là:
\(1950:\left(9+10+7\right).10=750\) (cây)
Số cây vải thiều là:
\(1950:\left(9+10+7\right).7=525\) (cây)
Đáp số: Quýt: 675 cây
Quýt: 750 cây
Vải: 525 cây
2. Một mảnh đất được chia thành 3 phần. Phần để xây nhà có diện tích chiếm \(\dfrac{3}{5}\) diện tích mảnh đất. Phần để làm sân có diện tích bằng 24% diện tích mảnh đất, phần diện tích còn lại là 24m2 để trồng cây cảnh.
a) Tính diện tích mảnh đất
Phân số chỉ phần diện tích còn lại để trồng cây cảnh là:
\(1-\dfrac{3}{5}-24\%=\dfrac{4}{25}\) (tổng số đất)
Diện tích mảnh đất là:
\(24:\dfrac{4}{25}=150m^2 \)
b) Tính diện tích phần đất để làm nhà
Diện tích phần đất để làm nhà là:
\(150.\dfrac{3}{5}=90m^2\)
Đáp số: a) \(150m^2\)
b) \(90m^2\)

Chọn D.
Phương pháp:
+) Sử dụng công thức tỉ lệ thể tích:
Cho khối chóp S.ABC, các điểm A 1 , B 1 , C 1 lần lượt thuộc SA, SB, SC
+) Chia khối chóp đã cho thành các khối chóp nhỏ, tính thể tích của từng khối chóp.
Cách giải:
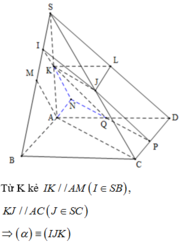
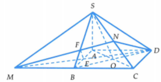
I,J lần lượt là trung điểm của SM, SC (do K là trung điểm của SA)
Trong (SAB), gọi N là giao điểm của IK và AB
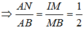
Trong (ABCD), kẻ đường thẳng qua N song song AC, cắt AD tại Q, CD tại P.
Khi đó, dễ dàng chứng minh P, Q lần lượt là trung điểm của CD, AD và

*) Gọi L là trung điểm của SD
Khi đó, khối đa diện SKJPQD được chia làm 2 khối: hình lăng trụ tam giác KJL.QPD và hình chóp tam giác S.KJL


Chọn đáp án C
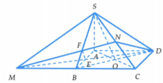
Gọi O là giao điểm của AC và BD
Ta có
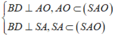
![]()
![]()
⇒ Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MND) là tứ giác DEFN.
Suy ra V 1 = V S . A D E F N và V 2 = V B C D E F N
Từ giả thiết ta có ∆ A B D đều cạnh a
![]()
Thể tích khối chóp N.MCD là
V N . M C D = 1 3 d N ; M C D . S ∆ M C D = a 3 4
Ta có F là trọng tâm của ∆ S M C nên M F M N = 2 3 ; E là trung điểm của MD nên M E M D = 1 2
Áp dụng công thức tính thể tích ta có:
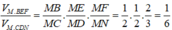
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S A B C D = a 3 4
Suy ra V 1 = V S . A D E F N = V S . A B C D - V 2 = a 3 24
Vậy V 1 V 2 = 1 5




Đáp án D.
Thể tích khối chóp cụt A B C . A ' B ' C ' được tính bằng công thức
V = h 3 B + B ' + B B ' = h 3 + 4 + 9 + 4.9 = 19 3 h
Thể tích của phần được tính bằng công thức V 1 = 1 3 . h .4 = 4 3 h
Tỉ số thể tích giữa ( H 1 ) và ( H 2 ) là 4 3 h 19 3 h − 4 3 h = 4 15 . Ta chọn D.