Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\widehat{A}_1=\widehat{C}_2;\widehat{A}_2=\widehat{C}_1;\widehat{B}=\widehat{D}\)
Các số nguyên tố có một chữ số là : 2, 3, 5, 7
Điền vào dấu hỏi chấm ta được
Trong các phân số trên, các phân số viết được dưới dạng số thập phân hữu hạn là:
Vậy có thể điền ba số: 2, 3, 5
Với mọi x thuộc R Có (x^2-9)^2 \(\ge\) 0
[y-4] \(\ge\) 0
Suy ra (x^2-9)^2+[y-4] - 1 \(\ge\) -1
Xét A=-1 khi và chỉ khi (x^2-9)^2 và [y-4] đều bằng 0
Tự tính ra
Xin lỗi nhưng vì không biết nên mình phải dùng [ ] thay cho GTTĐ nhé
Xin lỗi nhiều tại mình o tìm được kí hiệu đó
|
Câu |
Đúng | Sai |
| a) Các số 7,5 và 12 là các ngọai tỉ | X | |
| b) Các số 4 và 7,5 là các trung tỉ | X | |
| c) Các số 4 và 22,5 là các trung tỉ | X | |
| d) Các số 22,5 và 12 là các trung tỉ | X | |
| e) Các số 7,5 và 22,5 là các ngoại tỉ | X |
| Câu | Đúng | Sai |
| a)Các số 7,5 và 12 là các ngoại tỉ | X | |
| b)Các số 4 và 7,5 là các trung tỉ | X | |
| c)Các số 4 và 22,5 là các trung tỉ | X | |
| d)Các số 22,5 và 12 là các trung tỉ | X | |
| e)Các số 7,5 và 22,5 là các ngoại tỉ | X |
Ta có :
+) \(b^2=ac\Leftrightarrow\dfrac{a}{b}=\dfrac{c}{d}\) \(\left(1\right)\)
+) \(c^2=b.d\Leftrightarrow\dfrac{b}{c}=\dfrac{c}{d}\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
Đặt :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{d}=\dfrac{a}{d}=k^3\)
Mặt khác :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=k^3\)
Áp dụng tính chất dãy tỉ lệ thức ta có :
\(\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}=k^3\)
\(\Leftrightarrow\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}=\dfrac{a}{d}\rightarrowđpcm\)
Từ a/b=c/d⇒a/c=b/d
Áp dụng tính chất dãy tỉ số bằng nhau
a/c=b/d=a+b/c+d
⇒a^3/c^3=b^3/d^3=(a+b)^3/(c+d)^3 (1)
Từ a^3/c^3=b^3/d^3=a^3-b^3/c^3-d^3 (2)
Từ (1) và (2)
⇒(a+b)^3/(c+d)^3=a^3-b^3/c^3-d^3
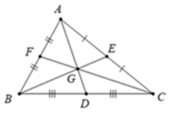
Ta có A D ; B E ; C F là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Theo tính chất ba đường trung tuyến của tam giác ta có: A G A D = 2 3 ⇒ A G G D = 2 ⇒ A G = 2 G D
Vậy số thích hợp điền vào chỗ chấm là: 2
Chọn đáp án A.