PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 5 2017
a)
b)4 bộ điểm thẳng hàng là
A,B,D,G; A,N,K,I; C,B,N,M; C,W,H,I; M,R,H,G
c) Năm đường thẳng cắt nhau từng đôi một có nhiều nhất 10 giao điểm
d)Vẽ 1 hình khác có 5 đường thẳng cắt nhau từng đôi một có 10 giao điểm
LH
20 tháng 5 2017
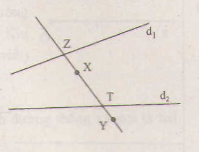
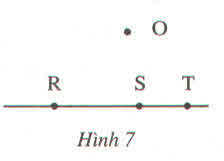
O..\(\notin\)..đường thẳng RS
R..\(\in\)..đường thẳng ST
S ..\(\notin\)....đường thẳng OT
T...\(\in\)..đường thẳng SR
SG
1
LS
18 tháng 4 2017
- Trong hình còn 4 điểm chưa đặt tên (mỗi dấu chấm biểu diễn một điểm). Ta sử dụng 4 chữ cái in hoa để đặt tên cho các điểm này, chẳng hạn A, B, C, D.
- Trong hình còn 2 đường thẳng chưa đặt tên. Ta sử dụng 2 chữ cái thường để đặt tên cho các đường này, chẳng hạn b, c.
LG
15 tháng 7 2017
Ta có \(A=3+3^2+3^3+3^4+....+3^{60}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{59}+3^{60}\right)\)
\(=4.3+4.3^3+...+4.3^{59}\)
\(=4.\left(3+3^3+...+3^{59}\right)⋮4\)
\(\Rightarrow A⋮4\)
13 ; 26 ; 52 cũng tương tự nha bạn!!
LG
15 tháng 7 2017
Bài 2: Có tất cả:
(6 . 5) : 2 = 15 (đường thẳng)
Bài 3: Có 6 điểm như trên bài 2.
Bài 4:Theo đề, ta có:
\(\left[n.\left(n-1\right)\right]:2=21\)
\(n.\left(n-1\right)=42\)
\(n.\left(n-1\right)=6.7\Rightarrow n=6\)
~ Học tốt ~
13 tháng 10 2016
Sơ đồ minh họa:
A B C G D E
\(S_{BCD}=\frac{1}{3}S_{ABC}\) (1) ( Chung chiều cao hạ từ \(C\) xuống \(AB\) và có đáy \(BD=\frac{1}{3}=AB\) do \(AD\) gấp đôi \(DB\) ). \(S_{BCE}=\frac{1}{3}S_{ABC}\) (2) ( Chung chiều cao hạ từ \(B\) xuống \(AC\) và có đáy \(EC=\frac{1}{3}AC\) do \(AE\) gấp đôi \(EC\) ).
Từ (1) và (2) \(\Rightarrow\) \(S_{BCD}=S_{BCE}\)
\(S_{BCD}-S_{BGC}=S_{GDB}\); \(S_{BCE}-S_{BGC}=S_{GEC}\)
Do đó \(S_{GDB}=S_{GEC}\)
. ai làm được mình sẽ tick.10 lần
5 tháng 8 2016
Ta có định lí :
Một điểm trên một đường thẳng thì có hai tia đối nhau.
Vậy theo đề bài ta có :
5 . 2 = 10 (cặp)
G
23 tháng 1 2019
a) Ta chia hình vuông thành 4 phần bằng nhau, sau đó tô 1 phần:
b) Ta chia hình chữ nhật ra 3 phần bằng nhau, sau đó tô 2 phần:
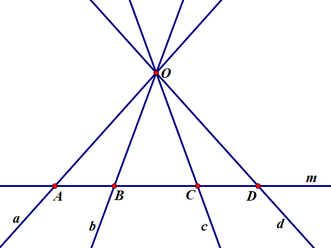
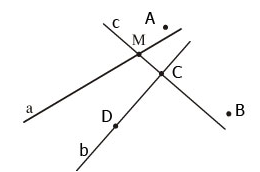
Các cách gọi tên đường thẳng:
- Đường thẳng a; đường thẳng AO, đường thẳng OA.
- Đường thẳng b; đường thẳng BO, đường thẳng OB.
- Đường thẳng c; đường thẳng CO, đường thẳng OC.
- Đường thẳng d; đường thẳng DO, đường thẳng OD.
- Đường thẳng m; đường thẳng AB; đường thẳng BA; đường thẳng AC; đường thẳng CA;