Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
+ Gọi C là hình chiếu của A lên mặt đáy chứa đường tròn O ' ; R và D là hình chiếu của B lên mặt đáy chứa đường tròn (O;R).
+) Tính thể tích lăng trụ đứng O A D . O ' C B , từ đó suy ra thể tích tứ diện OO'AB và đánh giá.
Cách giải:
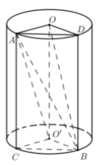

Chọn: D

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Đáp án A
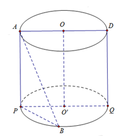
Gọi P là hình chiếu của A trên đáy O ' . Khi đó
A B = A P 2 + P B 2 = h 2 + B P 2 = 4 R 2 + P B 2 ≤ 4 R 2 + 4 R 2 = 2 R 2
Dấu bằng xảy ra ⇔ B P = P Q = 2 R .

Lấy điểm A ' ∈ O ' ; B ' ∈ O sao cho A A ' ; B B ' song song với trục O O ' .
Khi đó ta có lăng trụ đứng O A B ' . O ' A ' B .
Ta có:
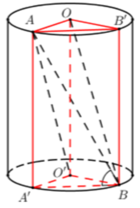
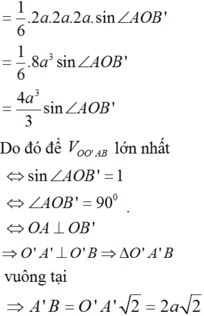
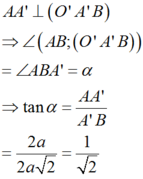
Chọn A.

Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P). Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.

Đáp án B
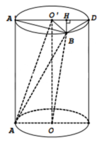
Kẻ đường sinh AA’, gọi D là điểm đối xứng A’ qua tâm O’.
Kẻ BH vuông góc với A ' D ⇒ B H ⊥ A O O ' A ' ⇒ V O O ' A B = 1 3 . B H . S Δ O O ' A
Mà S Δ O O ' A = 1 2 . O O ' . O A = 2 a 2 ⇒ V O O ' A B = 2 a 2 3 x B H
Để V O O ' A B lớn nhất ⇔ B H = B O ' H ≡ O ' ⇒ A ' B = 2 a 2
Tam giác AA’B vuông tại A’, có tan A B A ' ^ = A A ' A ' B = 2 a 2 a 2 = 1 2
Vậy A B ; O ' ^ = A B ; A ' B ^ = A B A ' ^ = α ⇒ tan α = 1 2
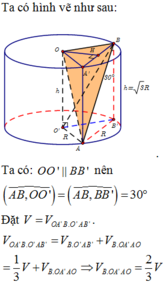

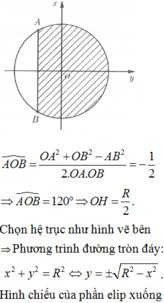


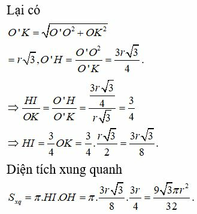
Chọn đáp án C.
Kẻ các đường sinh AA', BB' của hình trụ (T).
Khi đó
Như vậy, khối tứ diện có thể tích lớn nhất bằng