Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
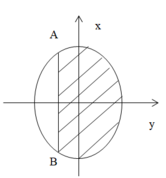
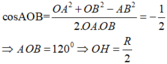
Chọn hệ trục tọa độ như hình vẽ => pt đường tròn đáy là:
![]()
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
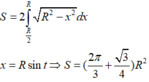
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
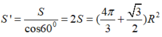

Đáp án C
Phương pháp:
+) Chứng minh mặt phẳng (P) không cắt đáy (O';R)
+) Tìm phần hình chiếu của mặt phẳng (P) trên mặt đáy. Tính S h c
+) Sử dụng công thức S h c = S . cos 60
Cách giải:
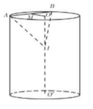
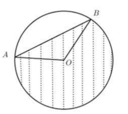
Gọi M là trung điểm của AB ta có:
O M = O A 2 − A B 2 2 = R 2 − 3 R 2 4 = R 2
Giả sử mặt phẳng (P) cắt trục OO’ tại I. Ta có : IA = IB nên Δ I A B cân tại I, do đó M I ⊥ A B


Vậy diện tích phần thiết diện cần tìm là :
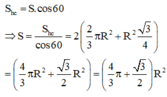

Đáp án D
cos A O B ^ = O A 2 + O B 2 - A B 2 2 . O A . O B = - 1 2 ⇒ A O B ^ = 120 0 ⇒ O H = R 2
Chọn hệ trục tọa độ như hình vẽ pt đường tròn đáy là:
x 2 + y 2 = R 2 ⇔ y = ± R 2 - x 2
Hình chiếu của phần elip xuống đáy là miền gạch chéo như hình vẽ
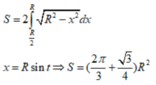
Gọi diện tích phần elip cần tính là S’. theo công thức hình chiếu ta có
S ' = S cos 60 0 = 2 S = ( 4 π 3 + 3 2 ) R 2

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P). Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.
Chọn đáp án D.