Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Bán kính đáy hình trụ bằng 2a. Mặt phẳng đi qua trục cắt hình trụ theo thiết diện là hình vuông Þ Chiều cao của hình trụ bằng đường kính đáy = 4a Thế tích khối trụ là: π 2 a 2 .4 a = 16 π a 3

Đáp án C.
ABCD là hình vuông với DC=2R=4cm từ đó Ad=4cm
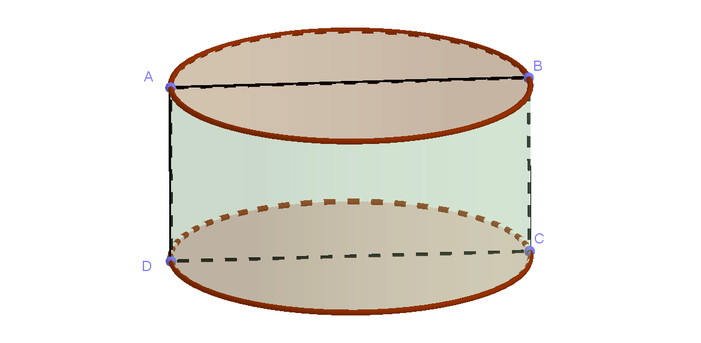
Từ đó: V H i n h = S d a y . A D = π 2 2 .4 = 16 π c m 2 .

a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.
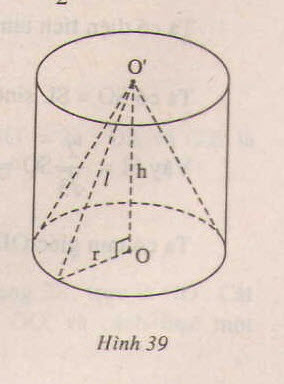

S A B C D = 8 a 2 ⇒ 2 a . h = 8 a 2 ⇔ h = 4 a
Diện tích xung quanh của hình trụ:
S x q = 2 πRh = 2 π . a . 4 a = 8 πa 2
Thể tích khối trụ
V t r ụ = πR 2 h = πa 4 . 4 a = 4 πa 3
Chọn đáp án C.

Đáp án C
Phương pháp:
Diện tích xung quanh của hình trụ ![]() và thể tích khối trụ
và thể tích khối trụ ![]()
Cách giải: Mặt phẳng qua trục cắt hình trụ theo thiết diện là hình chữ nhật có một cạnh là đường kính đáy và một cạnh là chiều cao của hình lăng trụ.
Gọi h là chiều cao của hình trụ ta có 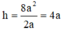
Vậy diện tích xung quanh của hình trụ ![]() và thể tích khối trụ
và thể tích khối trụ
![]()

Chọn C.
Phương pháp:
Tính chiều cao hình trụ và tính thể tích theo công thức


Đáp án B
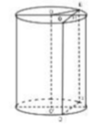
Gọi hình vuông thiết diện ABCD và O là tâm đường tròn đáy của hình trụ
Gọi H là trung điểm của AB, ta có
O H = a 2 ⇒ A H = O A 2 − A H 2 = a 2 − a 2 2 = a 3 2 ⇒ A B = a 3
Chiều cao của khối trụ chính là độ dài cạnh của hình vuông bằng h = a 3
Thể tích khối trụ là V = π r 2 h = π a 3 3


Chọn B.