Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Ta có BE = BA (gt) mà BA // CD và BA = CD (gt)
⇒ BE // CD và BE = CD.
Do đó BECD là hình bình hành nên F là trung điểm của BC.
Xét ΔBDC có I là trọng tâm ⇒ ID = 2IF.
b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.
c)ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:

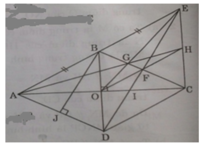
a) Ta có BE = BA (gt) mà BA // CD và BA = CD (gt)
⇒ BE // CD và BE = CD.
Do đó BECD là hình bình hành nên F là trung điểm của BC.
Xét ΔBDC có I là trọng tâm ⇒ ID = 2IF.

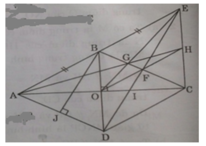
b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.
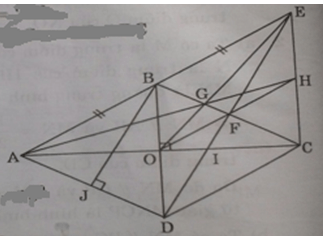
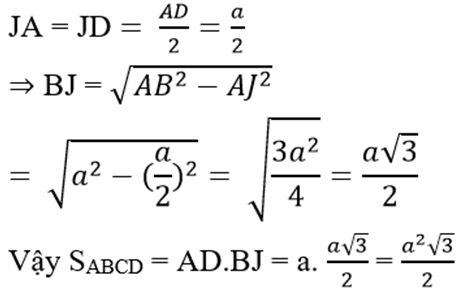
c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có: