Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)

S A B C D M N H K
Thế tích của khối chóp S.CDNM :
\(S_{CDNM}=S_{ABCD}-S_{AMN}-SBC\)
\(=AB^2-\frac{1}{2}AM.AN-\frac{1}{2}BC.BM\)
\(=a^2-\frac{a^2}{8}-\frac{a^2}{4}=\frac{5a^2}{8}\)
Vậy \(V_{SCDNM}=\frac{1}{3}S_{CDNM.SH}=\frac{5\sqrt{3}a^2}{24}\)
Khoảng cách giữa 2 đường thẳng DM và SC
\(\Delta ADM=\Delta DCN\Rightarrow\widehat{ADM}=\widehat{DCN}\Rightarrow DM\perp CN\)
Kết hợp với điều kiện :
\(DM\perp SH\Rightarrow DM\perp\left(SHC\right)\)
Hạ \(HK\perp SC\left(K\in SC\right)\Rightarrow HK\)là đoạn vuông góc chung của DM và SC
Do đó :
\(d\left(DM,SC\right)=HK\)
Ta có :
\(\begin{cases}HC=\frac{CD^2}{CN}=\frac{2a}{\sqrt{5}}\\HK=\frac{SH.HC}{\sqrt{SH^2+HC^2}}=\frac{2\sqrt{3}a}{\sqrt{19}}\end{cases}\)
\(\Rightarrow d\left(DM,SC\right)=\frac{2\sqrt{3}a}{\sqrt{19}}\)
cậu ơi, hướng dẫn giúp tớ bài tương tự này với: cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, góc giữa SD và mặt phẳng ABCD là 45 độ, SA vuông góc (ABCD). M là trung điểm BC. Tính khoảng cách DM và SC
cảm ơn c nhiều nhiều.

B A D C B1 C1 A1 F K E H
Gọi (\(\alpha\)) là mặt phẳng chứa DE và song song với \(A_1F\) thì khoảng cách cần tính bằng khoảng cách từ F đến ( \(\alpha\))
Theo giả thiết suy ra lăng trụ đã cho là lăng trụ đứng có đáy là tam giác đều cạnh a
Gọi K là trung điểm của \(FC_1\) thì \(EK\)//\(A_1F\)//AD, suy ra (\(\alpha\)) \(\equiv\left(ADKE\right)\)
Ta có \(A_1F\perp B_1C_1\Rightarrow A_1F\perp\left(BCC_1B_1\right)\) \(\Rightarrow EK\perp\left(BCC_1B_1\right)\)
Gọi H là hình chiếu vuông góc của F lên đường thẳng DK thì \(FH\perp\left(ADKE\right)\) suy ra FH là khoảng cách cần tính
Trong tam giác vuông DKF, ta có :
\(\frac{1}{FH^2}=\frac{1}{FD^2}+\frac{1}{FK^2}=\frac{1}{\left(\frac{a}{4}\right)^2}\Rightarrow FH=\frac{a}{\sqrt{17}}\)



Chọn đáp án C.
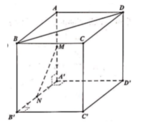
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa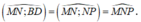
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên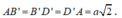
Suy ra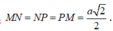
Do đó tam giác MNP đều