Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
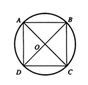
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông ABCD; R = a 2 2
Do đó thể tích hình trụ cần tìm bằng S = 2 πRh = 2 π a 2 2 a = πa 2 2 .

Đáp án D
Khối nón cần tìm có bán kính đáy r = a 2 2 ; chiều cao h = a .
Vậy diện tích xung quanh cần tính là S x q = π r l = π r h 2 + r 2 = 3 π a 2 2 .

Đáp án A
Bán kính đáy là R = a 2
Diện tích xung quanh hình trụ là S x q = 2 π R l = 2 π . a 2 .2 a = 4 π a 2 2

Đáp án A
Khối nón cần tìm có chiều cao h = a, bán kính đáy r = a 2 ⇒ l = h 2 + r 2 = a 5 2
Diện tích toàn phần của hình nón là S t p = S x q + S d = πrl + πr 2 = π . a 2 . a 5 2 + π a 2 2 .
= πa 2 4 5 + 1 = πa 2 4 b + c . Vậy b = 5 c = 1 → b c = 5 .

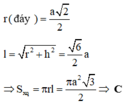

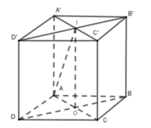

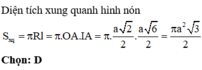
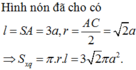

Đáp án là C
Hình nón cần tính diện tích xung quanh có chiều cao h = a, bán kính đáy