Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

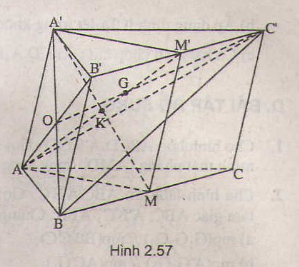
a) Do MM' lần lượt là trung điểm của BC và B'C' nên M'M//BB'//CC'. Vì vậy MM'//AA'.
Vì vậy tứ giác A'M'MA là hình bình hành. Suy ra: AM//A'M'.
b) Trong mp (AA'M'M), ta có: MA' ∩ AM' = K.
Do \(K\in A'M\) và \(A'M\in\left(AB'C'\right)\) nên K (AB'C').
c) Có \(O=AB'\cap A'B\) nên \(O\in\left(AB'C'\right)\cap\left(BA'C'\right)\).
Suy ra: \(d\equiv CO'\).
d) Trong (AB'C'): C'O ∩ AM' = G vì vậy G ( AMM') . Mà O, M' lần lượt là trung điểm AB' và B'C' nên G là trọng tâm của tam giác AB'C'.

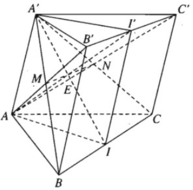
a) Ta có II′ // BB′ và II’ = BB’
Mặt khác AA′ // BB′ và AA’ = BB’ nên : AA′ // II′ và AA’ = II’
⇒ AA’II’ là hình bình hành.
⇒ AI // A′I′
b) Ta có:
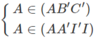
⇒ A ∈ (AB′C′) ∩ (AA′I′I)
Tương tự :
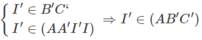
I′ ∈ (AB′C′) ∩ (AA′I′I) ⇒ (AB′C′) ∩ (AA′I′I) = AI′
Đặt AI′ ∩ A′I = E. Ta có:
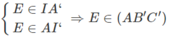
Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)
c) Ta có:
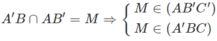
Tương tự:
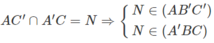
Vậy (AB′C′) ∩ (A′BC) = MN

a: Xét ΔAMB có ME là đường phân giác
nên AE/EB=AM/MB=AM/MC(4)
XétΔAMC có MD là đường phân giác
nên AD/DC=AM/MC(5)
Từ (4) và (5) suy ra AE/EB=AD/DC
b: Xét ΔABC có
AE/EB=AD/DC
nên ED//BC
Xét ΔABM có EI//BM
nên EI/BM=AE/AB(1)
Xét ΔACM có ID//MC
nên ID/MC=AD/AC(2)
Xét ΔABC có
ED//BC
nên AE/AB=AD/AC(3)
Từ (1), (2) và (3) suy ra EI/BM=DI/MC
mà BM=CM
nên EI=DI
hay I là trung điểm của ED

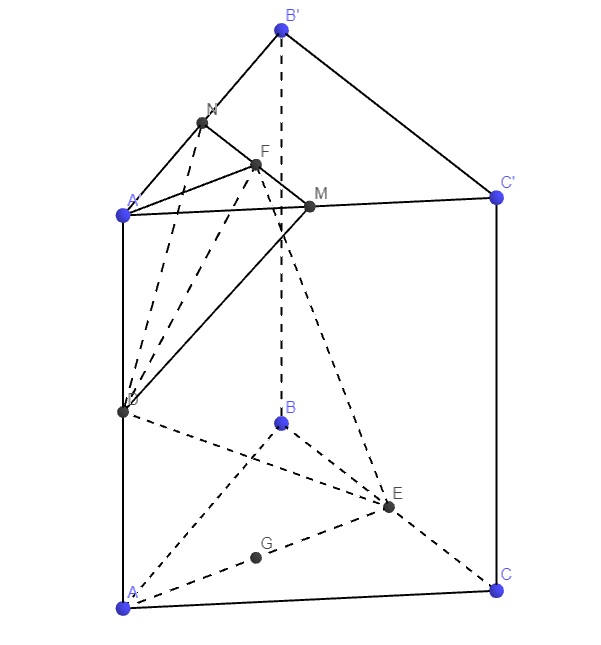
Gọi D, E, F lần lượt là trung điểm A'A, BC và MN
\(\left\{{}\begin{matrix}MN||B'C'\\DN||AB'\end{matrix}\right.\) (đường trung bình tam giác) \(\Rightarrow\left(AB'C'\right)||\left(DNM\right)\)
\(\Rightarrow\) Góc giữa (AB'C') bằng góc giữa (DNM) và (BCMN)
\(MN\perp A'F\) (A'MN là tam giác đều), và \(A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp MN\)
\(\Rightarrow MN\perp\left(A'AEF\right)\) \(\Rightarrow\) góc giữa (DNM) và (BCMN) là \(\widehat{DFE}\) nếu nó là góc nhọn và \(180^0-\widehat{DFE}\) nếu nó là góc tù
\(MN=\dfrac{1}{2}B'C'=\sqrt{3}\Rightarrow A'F=\dfrac{MN\sqrt{3}}{2}=\dfrac{3}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow DF=\sqrt{A'F^2+A'D^2}=\dfrac{\sqrt{13}}{2}\)
\(AE=\dfrac{AB\sqrt{3}}{2}=3\Rightarrow DE=\sqrt{AD^2+AE^2}=\sqrt{10}\)
Gọi G là trung điểm AE \(\Rightarrow FG\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}FG=A'A=2\\GE=\dfrac{1}{2}AE=\dfrac{3}{2}\end{matrix}\right.\)
\(EF=\sqrt{FG^2+EG^2}=\dfrac{5}{2}\)
Áp dụng định lý hàm cos:
\(cos\widehat{DFE}=\dfrac{DF^2+EF^2-DE^2}{2DF.EF}=...\Rightarrow\widehat{DFE}=...\)






a) Ta có tứ giác AA’CC’ là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.
Do đó IH // CB′ ( đường trung bình của tam giác CB’A’)
Mặt khác IH ⊂ (AHC′) nên CB′ // (AHC′)
b) Ta có:
suy ra, ⇒ A là điểm chung của (AB’C’) và (ABC)
Mà
Nên (AB′C′) ∩ (ABC) = Ax
Và Ax // BC // B′C′