Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng vectơ và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vector BB', CC', DD'.

Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AC}=\overrightarrow{b},\overrightarrow{AA'}=\overrightarrow{c}\)
với \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\)
và \(\left|\overrightarrow{a}\right|=a,\overrightarrow{\left|b\right|}=a\sqrt{2},\left|\overrightarrow{c}\right|=a\sqrt{3}\)
khi đó
\(\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{c,}\overrightarrow{BC}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Giả sử đường vuông góc chung cắt \(\overrightarrow{AB}\) tại M và cắt \(\overrightarrow{BC'}\) tại N và \(\overrightarrow{AM}=x.\overrightarrow{AB'}=x.\overrightarrow{a}+x.\overrightarrow{c},\overrightarrow{BN}=y.\overrightarrow{BC'}=-y.\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Suy ra \(\overrightarrow{AN}=\left(1-y\right)\overrightarrow{a}+y.\overrightarrow{b}+y.\overrightarrow{c}\)
Và do đó
\(\overrightarrow{MN}=\left(1-x-y\right)\overrightarrow{a}+y.\overrightarrow{b}+\left(y-x\right)\overrightarrow{c}\)
Ta có :
\(MN\perp AB',BC'\Leftrightarrow\begin{cases}\overrightarrow{MN}.\overrightarrow{AB}=0\\\overrightarrow{MN}.\overrightarrow{BC'}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}-4x+2y+1=0\\-2x+6y-1=0\end{cases}\)
Giải hệ ta thu được \(x=\frac{2}{5},y=\frac{3}{10}\)
Từ đó :
\(MN^2=\left[\left(1-x-y\right)^2+2y^2+3\left(y-x\right)^2\right].a^2=\frac{39^a}{100}\)
Suy ra \(d\left(AB';BC'\right)=\frac{a\sqrt{39}}{10}\)
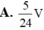
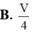
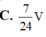
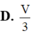
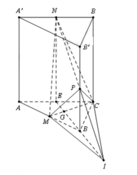

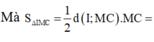

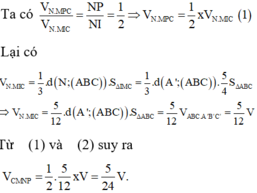



Đáp án B.
Xét ∆ AA'C có I là trọng tâm,
Ta có: