Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

11.
Thay tọa độ M vào pt d ta được:
\(\frac{1}{1}=\frac{3}{3}=\frac{m}{-2}\Rightarrow m=-2.1=-2\)
12.
\(AA'\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của A'B lên (ABC)
\(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và (ABC)
\(\Rightarrow\widehat{A'BA}=60^0\)
\(AB=\frac{AC}{\sqrt{2}}=2a\Rightarrow AA'=AB.tan60^0=2a\sqrt{3}\)
8.
\(I=2\int\limits^9_0f\left(x\right)dx+3\int\limits^9_0g\left(x\right)dx=2.37+3.???=...\)
Đề thiếu, bạn tự điền số và tính
9.
\(z=\frac{1}{3-4i}=\frac{3+4i}{\left(3-4i\right)\left(3+4i\right)}=\frac{3}{25}+\frac{4}{25}i\)
\(\Rightarrow\overline{z}=\frac{3}{25}-\frac{4}{25}i\)
10.
\(\overline{z_1}=1-5i\) \(\Rightarrow\overline{z_1}+iz_2=1-5i+i\left(3-2i\right)=3-2i\)
Điểm biểu diễn là \(Q\left(3;-2\right)\)

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A

4.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)
Lại có \(AK\perp SC\)
\(\Rightarrow SC\perp\left(AKH\right)\Rightarrow SK\) là đường cao của chóp S.AHK ứng với đáy là tam giác AHK vuông tại H (do \(AH\perp\left(SBC\right)\Rightarrow AH\perp HK\))
Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AB^2}=\)
À thôi đến đây phát hiện ra đề bài sai
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông tại A với SA là cạnh góc vuông, SB là cạnh huyền
\(\Rightarrow SB>SA\Rightarrow SB=SA=a\) là hoàn toàn vô lý
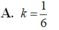
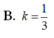
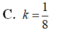
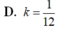
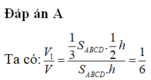


Đáp án A
Phương pháp:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
Cách giải: