Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ dãy tỉ số bằng nhau đó, ta được:
\(\frac{2a+b+c+d}{a}-1=\frac{a+2b+c+d}{b}-1=\frac{a+b+2c+d}{c}-1=\frac{a+b+c+2d}{d}-1\)
hay \(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}=\frac{4\left(a+b+c+d\right)}{a+b+c+d}=4\)
Do đó, \(\frac{a+b+c+d}{a}=4\) => a=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{b}=4\) =>b=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{c}=4\) =>c=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{d}=4\) => d=\(\frac{a+b+c+d}{4}\)
=>a=b=c=d
a+bc+d
Do đó, M=\(\frac{a+b}{c+d}+\frac{b+c}{c+d}+\frac{c+d}{a+b}+\frac{d+a}{b+c}=\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}=1+1+1+1=4\)
Vậy M có giá trị là 4



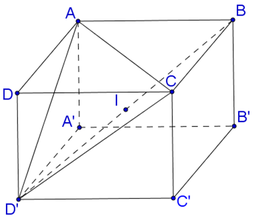

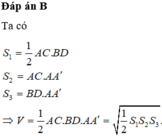
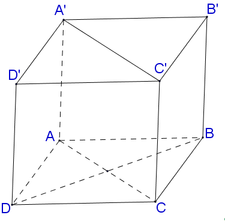
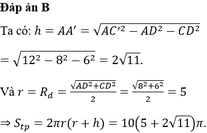
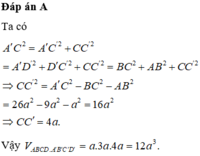
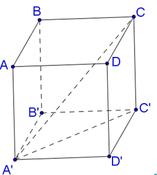
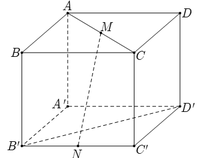

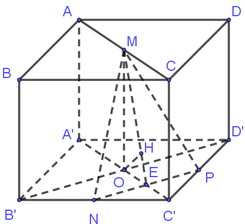
Đáp án A