Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A:
Đ O Δ O C F = Δ O A E V A ; 2 Δ O A E = Δ C A B
Đáp án B:
Đ A C Δ O C F = Δ O C M V C ; 2 Δ O C M = Δ A C B
Đáp án C:
V C ; 2 Δ O C F = Δ A C D Đ O Δ A C D = Δ C A B
Đáp án D:
Đ B D Δ O C F = Δ O A N V O ; − 1 Δ O A N = Δ O C M
Vậy phép đồng dạng P được hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O, tỉ số k = -1 không biến tam giác OCF thành tam giác CAB.
Đáp án D

Đ E I ( 1 ) = ( 8 ) ; T D I → ( 8 ) = ( 3 ) .
A. Phép đối xứng tâm I và phép đối xứng trục IB thì (1) không biến thành hình nào từ (2) đến (8).
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o (1) không biến thành hình nào từ (2) đến (8)
D.phép tịnh tiến theo A I → và phép đối xứng tâm I thì hình (1) thành hình (2)
Đáp án C

V ( C ; 2 ) ( I G H F ) = ( A I F D ) ; Đ I ( A I F D ) = C I E B .
Đáp án C.

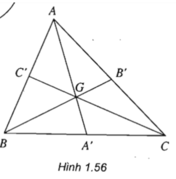
Theo đề bài ta có: AA', BB', CC' là các đường trung tuyến của ΔABC ⇒ G là trọng tâm
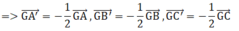
Vậy phép vị tự tâm G, tỉ số k = -1/2 biến tam giác ABC thành tam giác A'B'C'

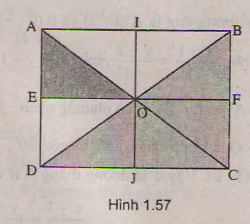
Phép đối xứng qua đường thẳng ***** biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
Phép đối xứng qua đường thẳng biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.

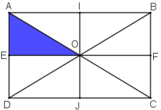
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
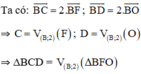
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.
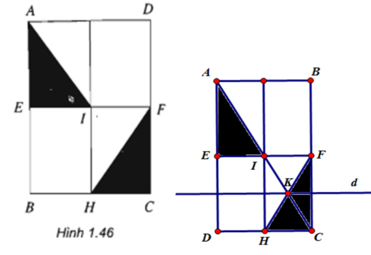



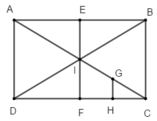
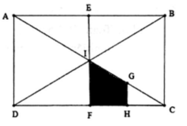
- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH