Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


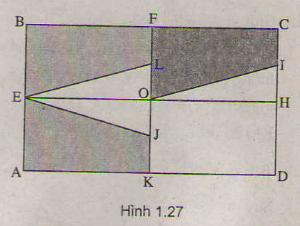
Gọi L là trung điểm của đoạn thẳng OF. Ta thấy phép đối xứng qua đường thẳng EH biến hình thang AEJK thành hình thang BELF, phép tịnh tiến theo vectơ BF biến hình thang BELF thành hình thang FOIC. Như vậy phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên, sẽ biến hình thang AEJK thành hình thang FOIC. Do đó hai hình thang AEJK và FOIC bằng nhau.
Gọi L là trung điểm của đoạn thẳng OF.
Ta thấy phép đối xứng qua đường thẳng EH biến hình thang AEJK thành hình thang BELF, phép tịnh tiến theo vectơ BF biến hình thang BELF thành hình thang FOIC. Như vậy phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên, sẽ biến hình thang AEJK thành hình thang FOIC. Do đó hai hình thang AEJK và FOIC bằng nhau.

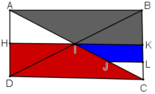
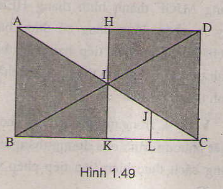
+ I là trung điểm AC; BD; HK
⇒ ĐI(H) = K ; ĐI(D) = B ; ĐI (C) = A.
⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)
+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA
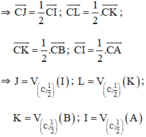
⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.
⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.
⇒ IJKI và IHDC đồng dạng.

Đáp án D
![]()
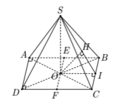
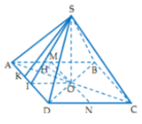
I là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥ (ABCD)
Từ đó ta chứng minh được
![]()
![]()
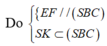
![]()
Tính được
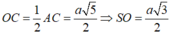
Suy ra
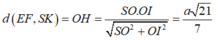

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

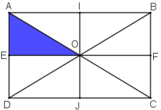
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
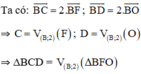
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.

Phép đối xứng qua đường thẳng ***** biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
Phép đối xứng qua đường thẳng biến tam giác AEO thành tam giác BFO, phép vị tự tâm B, tỉ số 2 biến tam giác BFO thành tam giác BCD. Do đó ảnh của tam giác AEO qua phép đồng dạng đã cho là tam giác BCD.
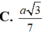
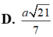

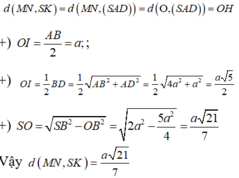
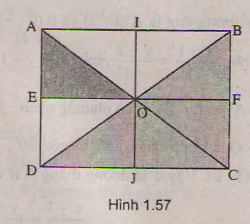
Gọi L là trung điểm của OF.
+ Vì EO là đường trung trực của các đoạn thẳng AB; KF; JL
⇒ B = ĐEO (A); F = ĐEO (K) ; L = ĐEO (J); E = ĐEO (E)
⇒ Hình thang BFLE là ảnh của hình thang AKJE qua phép đối xứng trục EO.
⇒ Hai hình thang BFLE và AKJE bằng nhau (1)
⇒ Hình thang FCIO là ảnh của hình thang BFLE qua phép tịnh tiến theo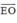
⇒ Hai hình thang FCIO và BFLE bằng nhau (2)
Từ (1) và (2) ⇒ hai hình thang FCIO và AKJE bằng nhau.