Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
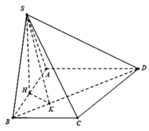
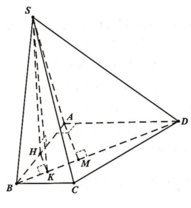
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: ![]()
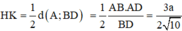
Do đó 
Vậy 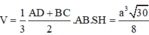

Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
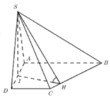
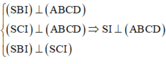
Kẻ IH
⊥
CD ta có: 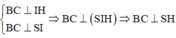
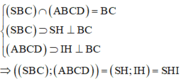
Ta có: 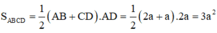
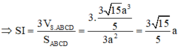
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
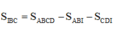
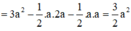
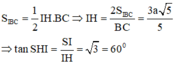


Đáp án C
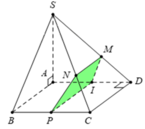
Kẻ I M ⊥ S D tại M Đường thẳng I M ⊂ m p P
ABCD là hình vuông ⇒ C D ⊥ A D mà S A ⊥ C D ⇒ C D ⊥ S A D
Ta có P ⊥ A D mà C D ⊥ A D ⇒ C D / / m p P
Qua I kẻ đường thẳng song song với CD, cắt BC tại P
Qua M kẻ đường thẳng song song với CD, cắt SC tại N
Suy ra mặt phẳng (P) cắt khối chóp S.ABCD theo thiết diện là hình thang vuông IMNP tại M và I.
Tam giác SAD vuông tại A có d A ; S D = a 3 ⇒ I M = a 3 2
Tam giác IMD vuông tại M có M D = I D 2 − I M 2 = a 2 ⇒ S M S D = 7 8 ⇒ M N = 7 a 4
Vậy diện tích hình thang IMNP là S = I M . M N + I P 2 = a 3 2 . 1 2 . 7 a 4 + 2 a = 15 3 16 a 2

Đáp án C
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6
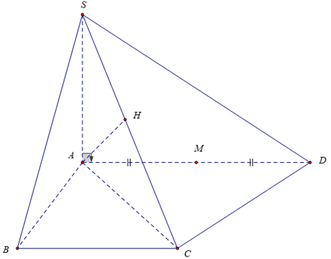

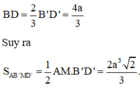

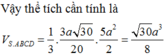

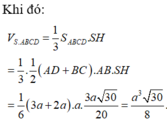
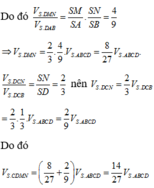
Đáp án A.
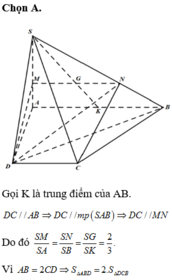
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .