Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này ứng dụng 1 phần cách giải của bài này:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
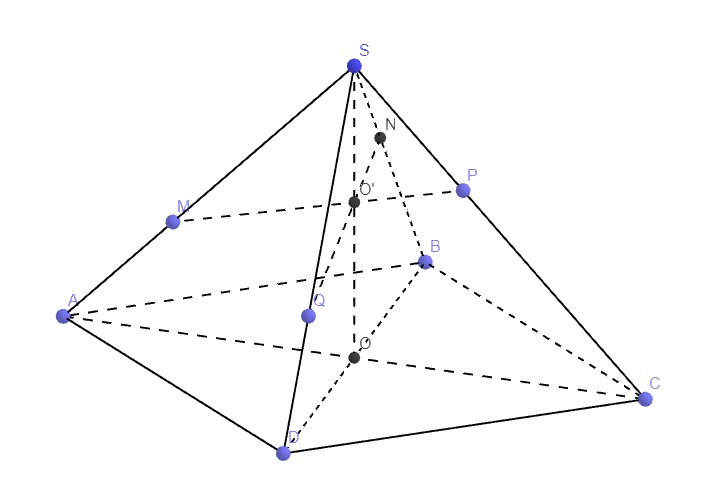
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)

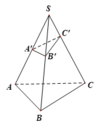
Mặt phẳng (SAC) và (SBD) cắt nhau bởi giao tuyến SO
Mặt phẳng (SAC) và (MNPQ) cắt nhau bởi giao tuyến MP
Mặt phẳng (SBD) và (MNPQ) cắt nhau bởi giao tuyến NQ
\(\Rightarrow\) 3 mặt phẳng (SAC), (SBD), (MNPQ) cắt nhau theo 3 giao tuyến phân biệt MP, NQ, SO nên 3 đường thẳng này đồng quy
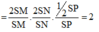


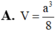
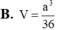
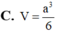
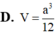
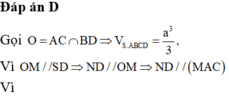
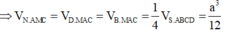
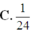
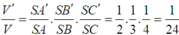
Đáp án là A