Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà


Chọn B.
Phương pháp:
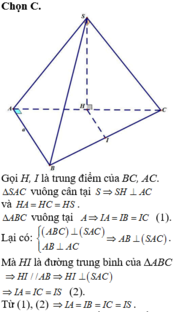
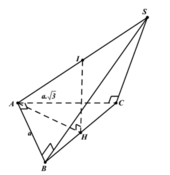
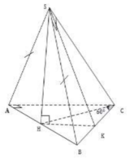
+ Gọi H là trung điểm BC. Ta chứng minh A H ⊥ A B C và AH là trục đường tròn ngoại tiếp tam giác
SBC
+ Suy ra tâm mặt cầu ngoại tiếp chóp S. ABC là giao của AH và đường trung trực cạnh AB.
+ Chỉ ra tam giác SBC vuông tại S từ đó tính SC theo định lý Pytago.
Cách giải:
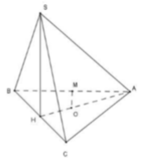




Đáp án C

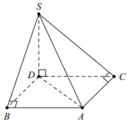
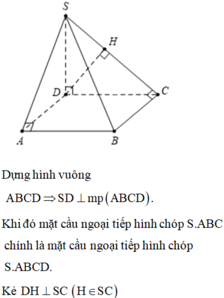
Kẻ hinh chữ nhật A B C D như hình vẽ bên ⇒ S D ⊥ A B C D
Diện tích tam giác ABC là S A B C = 1 2 . A B . A C = a 2
Suy ra V S . A B C = 1 3 . S D . S Δ A B C = a 2 3 . S D = 2 3 a 3 ⇒ S D = 2 a .
Bán kính mặt cầu ngoại tiếp khối chóp S . A B D C là
R = R A B D C 2 + S D 2 4 = a 5 2 2 + 2 a 2 4 = 3 a 2
Vậy bán kính mặt cầu cần tính là R = 3 a 2 .
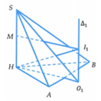


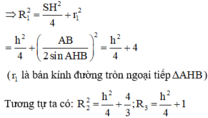


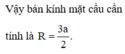





Đáp án B
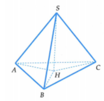
Gọi H là trung diểm của BC suy ra cos A C B ^ = sin H A B ^ = 1 3 ⇒ cos H A B ^ = 2 2 3
Mà sin B A C ^ = 2 sin H A B ^ . cos H A B ^ = 4 2 9 nên theo định lí Sin, ta có R ∆ A B C = B C 2 s i n B A C ^ = 9 4
Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là R = R 2 ∆ A B C + S A 2 4 = a 97 4
Vậy diện tích mặt cầu cần tính là S = 4 πR 2 = 4 π a 97 4 2 = 97 πa 2 4