Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
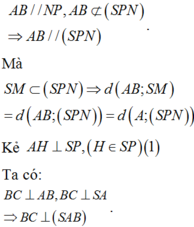
Mà
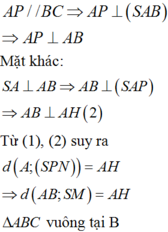
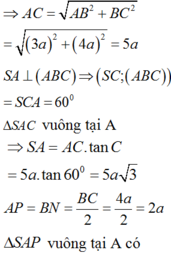
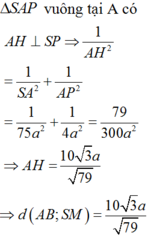
Chọn: B

Đáp án D
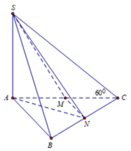
Gọi N là trung điểm của BC
Ta có A B / / M N ⇒ d A B ; S M = d A ; S M N
S A = A C tan 60 ° = 5 a 3
S M = 5 a 3 2 + 5 a 2 2 = 5 a 13 2
S N 2 = S B 2 + B N 2 = S A 2 + A B 2 + B C 2 2 = 5 a 3 2 + 3 a 2 + 2 a 2 = 88 a 2
⇒ S N = 2 a 22
M N = A B 2 = 3 a 2
Ta có:
S M 2 = N S 2 + N M 2 − 2 N S . N M . c o s M N S ^ ⇔ 5 a 13 2 22 = 88 a 2 + 3 a 2 2 − 2.2 a . 22 . 3 a 2 c o s M N S ^
c o s M N S ^ = 3 2 22 ⇒ sin M N S ^ = 79 88
S S M N = 1 2 N M . N S . s i n M N S ⏜ = 1 2 . 3 a 2 .2 a 22 . 79 88 = 3 a 2 79 4
S A M N = 1 4 S A B C = 1 4 . 1 2 .3 a .4 a = 3 a 2 2 ; V S . A M N = 1 3 S A . S A M N = 1 3 .5 a 3 . 3 a 2 2 = 5 a 3 3 2
d A ; S M N = 3 V S . A M N S S M N = 3. 5 a 3 3 2 3 a 2 79 4 = 10 a 3 79

Đáp án A

Do S A ⊥ A B C nên góc giữ SC và A B C là góc S C A ^ = 60 °
Vì Δ A B C vuông tại B nên A C = 5 a ⇒ S A = 5 a 3
Gọi N là trung điểm BC nên M N / / A B ⇒ A B / / S M N
d A B , S M = d A B , S M N = d A , S M N .
Từ A kẻ đường thẳng song song vơi BC cắt MN tại D.
Do B C ⊥ A B ⇒ B C ⊥ M N ⇒ A D ⊥ M N .
Từ A kẻ AH vuông góc vơi SD
Ta có M D ⊥ A D M D ⊥ S A ⇒ M D ⊥ S A D ⇒ M D ⊥ A H
Mà A H ⊥ S D ⇒ A H ⊥ S M D hay A H ⊥ s m n ⇒ d A , S M N = A H
Do A D = B N = 1 2 B C = 2 a .
Xét Δ S A D có 1 A H 2 = 1 S A 2 + 1 A D 2 = 1 75 a 2 + 1 4 a 2 = 79 300 a 2
⇒ d A B , S M = A H = 10 237 a 79 = 10 3 a 79

Đáp án D
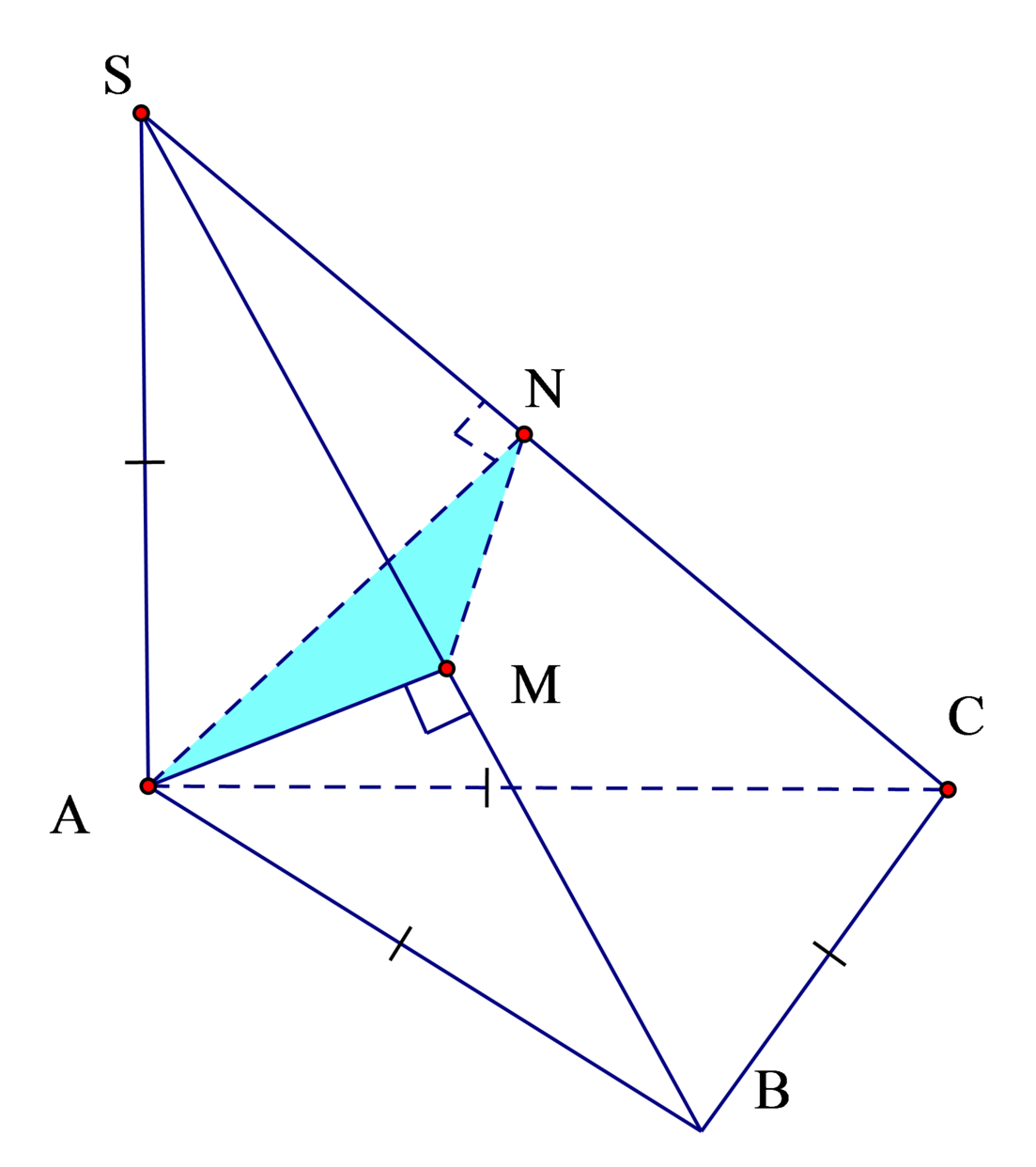
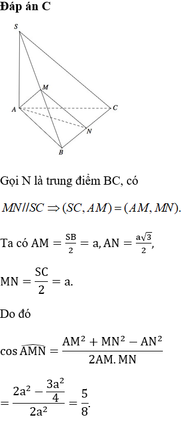
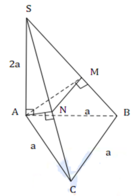
Do Δ S A B , Δ S A C cân nên M, N là trung điểm SB, SC
Ta có: V S . A M N V S . A B C = S M S B S N S C = 1 2 1 2 = 1 4 ⇒ V A . B C M N V S . A B C = 3 4
⇒ V A . B C M N = 3 4 V S . A B C = 1 4 S A . d t A B C = 1 4 a . a 2 3 4 = a 3 3 16


Chọn B.
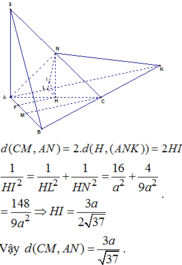
Gọi E là trung điểm của MC. Qua A kẻ một đường thẳng song song với BC cắt đường thẳng NE tại K.
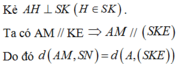
Ta dễ chứng minh được A H ⊥ S K E nên d A ; S K E = A H . Tam giác SAKvuông ở A và có AH là đường cao nên
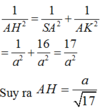

Đáp án B
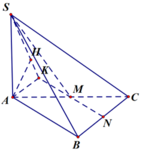
Gọi N là trung điểm của BC.
d A B , S M = d A , S M N
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được A H ⊥ S M N tại H, suy ra d A B , S M = d A , S M N = A H
A K = B N = 2 a , S A = 5 a 3 ⇒ A H = 10 a 3 79
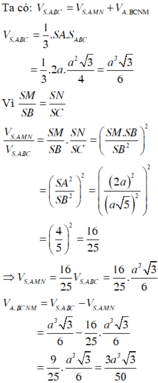
Đáp án A.
Phương pháp:
- Phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng trong không gian:
d Δ 1 ; Δ 2 = M 1 M 2 → . u 1 → ; u 2 → u 1 → ; u 2 → , M 1 ∈ Δ 1 ; M 2 ∈ Δ 2
Cách giải:
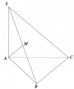
Gắn hệ trục tọa độ (như hình vẽ):
A 0 ; 0 ; 0 , B 0 ; a ; 0 , C a 3 2 ; a 2 ; 0 , S 0 ; 0 ; 3 a
M, N lần lượt là trung điểm của AB, SC
⇒ M 0 ; a 2 ; 0 , N a 3 4 ; a 4 ; 3 a 2
⇒ A N → = a 3 4 ; a 4 ; 3 a 2 ; C M → = − a 3 2 ; 0 ; 0
Đường thẳng AN có 1 VTCP u 1 → = 3 ; 1 ; 6 ,
đi qua điểm A 0 ; 0 ; 0 .
Đường thẳng CM có 1 VTCP u 1 → = 1 ; 0 ; 0 , đi qua điểm A 0 ; a 2 ; 0 .
A M → = 0 ; a 2 ; 0 , u 1 → ; u 2 → = 0 ; 6 ; − 1
d A N ; C M = A M → . u 1 → ; u 2 → u 1 → ; u 2 → = 0.0 + a 2 .6 + 0. − 1 0 2 + 6 2 + 1 2 = 3 a 37