Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
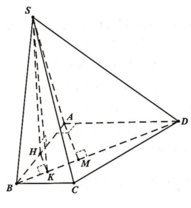
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà


Đáp án D
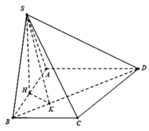
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: ![]()
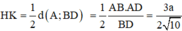
Do đó 
Vậy 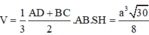

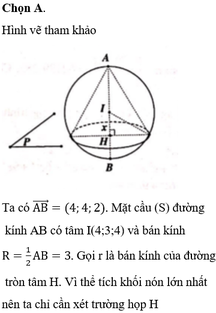
Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
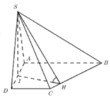
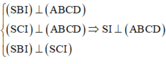
Kẻ IH
⊥
CD ta có: 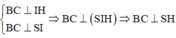
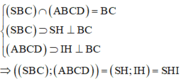
Ta có: 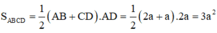
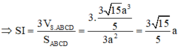
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
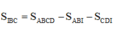
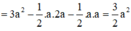
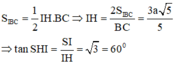


Đáp án C

Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM//SA
![]()
=> OM là trục của đường tròn ngoại tiếp tam giác ABC,
=> OA = OB = OC
Mặt khác, tam giác SAC vuông tại A, do đó OA = OS = OC
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ABC có thể tích 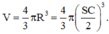
A là hình chiếu của S lên mặt phẳng (ABC), do đó góc ![]()
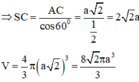

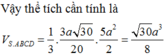

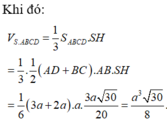
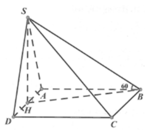


+Vì S A B ⊥ A B C D , S A D ⊥ A B C D mà S A B ∩ S A D = S A nên S A là đường cao của khối chóp
+ Xét tam giác vuông S A C
S A = tan 60 o . A C = 3 . a . 5 = a 15