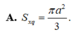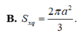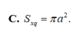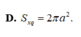Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
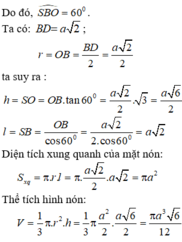

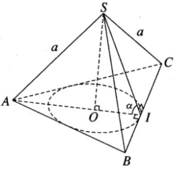
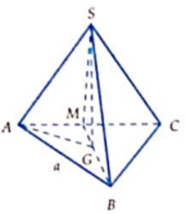
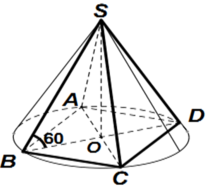
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 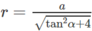
Hình nón nội tiếp có đường sinh là :
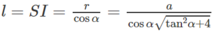
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
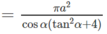

Đáp án C
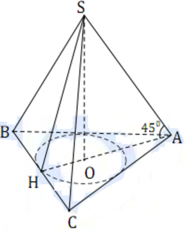
Gọi O là tâm đường tròn nội tiếp ∆ ABC.Theo giả thiết, góc giữa cạnh bên và đáy chính là góc giữa SA và OA hay S A O ^ = 45 o .Diện tích xung quanh cần tính là: S x q = π R l
Tam giác ABC đều cạnh 2a nên AH =a 3
Suy ra:
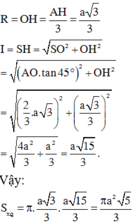

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow\widehat{SAO}=60^0\)
\(AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(S_{xq}=\pi.AO.SA=\dfrac{2\pi a^2}{3}\)

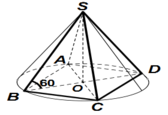
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)
\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)