Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
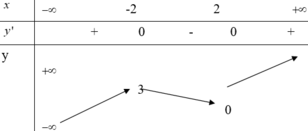
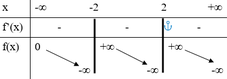
Hàm số xác định 
vì đường thẳng y=0 cắt đồ thị f(x) tại hai điểm có hoành độ x=a<-2; x=2
Ta có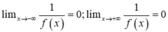 
⇒ y = 0 là tiệm cận ngang duy nhất.
Và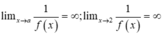 
⇒ x = a ; x = 2 là các đường tiệm cận đứng.
Vậy đồ thị hàm số có tổng 3 đường tiệm cận ngang và đứng.
Chọn đáp án B.
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
Đáp án là D
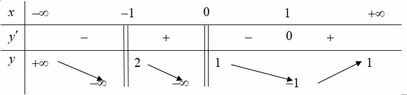
Từ BBT ta có
lim x → + ∞ y = − 1 ; lim x → − ∞ y = 1 do đó đồ thị hàm số có hai đường tiệm cận ngang là
y = 1; y =−1.
lim x → 1 − y = + ∞ ; lim x → 1 − y = − ∞ do đó đồ thị hàm số có một đường tiệm cận đứng là x =1. Vậy tổng số có 3 đường tiệm cận
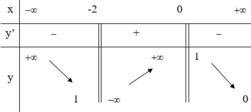
HD: Đồ thị hàm số có tiệm cận đứng là x = -2 và x = 0, tiệm cận ngang là y = 0. Chọn B.
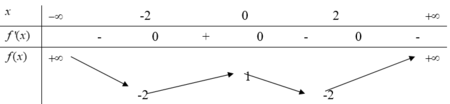
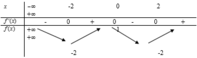
TCN: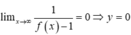
là tiệm cận ngang duy nhất;
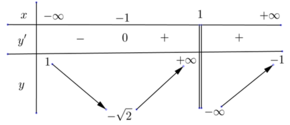
TCĐ: Hàm số xác định ⇔ f ( x ) - 1 # 0 ⇔ f ( x ) # 1
(vì đồ thị f(x) cắt đường thẳng y = 1 tại ba điểm có hoành độ lần lượt x=a<-2;x=0;x=b>2).
Có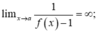
⇒ x = a ; x = 0 ; x = b là tiệm cận đứng.
Vậy đồ thị hàm số y = 1 f ( x ) - 1 có tổng 4 đường tiệm cận đứng và ngang.
Chọn đáp án B.