

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Ta có: y ' = − 1 − m x − 1 2
· Trường hợp 1: nếu y ' > 0 ⇒ m < − 1 , lúc này hàm số đồng biến
⇒ min 2 ; 4 y = y 2 = 2 + m 2 − 1 = 3 ⇒ m = 1 (mâu thuẫn với m < -1) => loại
· Trường hợp 2: nếu y ' < 0 ⇒ m > − 1 , lúc này hàm số nghịch biến
⇒ min 2 ; 4 y = y 4 = 4 + m 4 − 1 = 3 ⇒ m = 5 (thỏa mãn với m > -1) => chọn
Đối chiếu 4 đáp án thì có đáp án C là thỏa mãn.

Đáp án C
Phương pháp: Hàm số bậc nhất trên bậc nhất y = a x + b c x + d a d - b c ≠ 0 luôn đơn điệu trên từng khoảng xác định của nó.
TH1: Hàm số đồng biến trên [2;4] => m a x 2 ; 4 y = y ( 4 )
TH2: Hàm số nghịch biến trên [2;4] => m a x 2 ; 4 y = y ( 2 )
Cách giải: Tập xác định: D = R\{1}
Ta có: 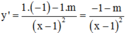
TH1: ![]()
![]() =>Hàm số đồng biến trên
=>Hàm số đồng biến trên 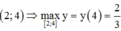
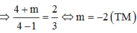
TH2: ![]()
![]() => Hàm số nghịch biến trên
=> Hàm số nghịch biến trên ![]()
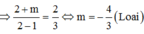
Vậy m = –2
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn

Đáp án C
Có y ' = m 2 + 1 x + m > 0 ∀ x ∈ D . Vậy max 1 ; 4 y = y 4 = 4 m − 1 4 + m = 1 ⇔ m = 5 3 ∈ 1 ; 2

Đáp án B
Ta có: y ' = − x 2 + 2 x − 3 < 0 ⇒ hàm số nghịch biến trên đoạn 0 ; 3 .
Do đó M a x 0 ; 3 y = y 0 = m = − 7

Câu 1 :
Đk: \(x\ge1\)
\(\sqrt{x-1}+\sqrt{2x-1}=5\\ \Leftrightarrow x-1+2\sqrt{\left(x-1\right)\left(2x-1\right)}+2x-1=25\\ \Leftrightarrow2\sqrt{2x^2-3x+1}=27-3x\\ \)
\(\Leftrightarrow\begin{cases}27-3x\ge0\\4\left(2x^2-3x+1\right)=9x^2-162x+729\end{cases}\) \(\Leftrightarrow\begin{cases}x\le9\\x^2-150x+725=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\le9\\x=145hoặcx=5\end{cases}\)
với x= 5 thoản mãn điều kiện, x=145 loại
Vậy \(S=\left\{5\right\}\)