Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Điều kiện \(D=\left(-\infty;0\right)U\left(1;+\infty\right)\)
\(y'=\frac{\sqrt{x^2-x}-x.\frac{2x-1}{2\sqrt{x^2-x}}}{x^2-x}=\frac{-x}{2\left(x^2-x\right)\sqrt{x^2-x}}\)
Ta thấy \(y'< 0\) trên \(\left(1;+\infty\right)\), suy ra hàm số nghịch biến trên \(\left(1;+\infty\right)\).
Câu 2:
\(y'=1+\frac{2x}{\sqrt{2x^2+1}}=\frac{2x+\sqrt{2x^2+1}}{\sqrt{2x^2+1}}\)
Xét bất phương trình:
\(2x+\sqrt{2x^2+1}< 0\)
\(\Leftrightarrow\sqrt{2x^2+1}< -2x\)
\(\Leftrightarrow\hept{\begin{cases}x< 0\\2x^2+1< 4x^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 0\\x< \frac{-\sqrt{2}}{2}\left(h\right)x>\frac{\sqrt{2}}{2}\end{cases}}\Leftrightarrow x< \frac{-\sqrt{2}}{2}\)
Vậy hàm số nghịch biến trên \(\left(-\infty;\frac{-\sqrt{2}}{2}\right)\).

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3
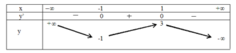

 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.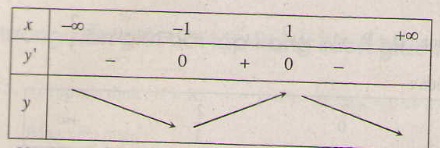



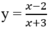
Đáp án là D
Từ bảng biến thiên ta có: hàm số nghịch biến trên khoảng - ∞ ; - 1 và 1 ; + ∞ , hàm số đồng
biến trên khoảng (-1;1).