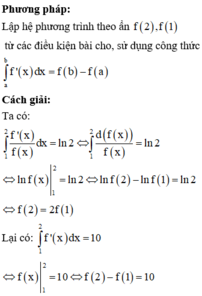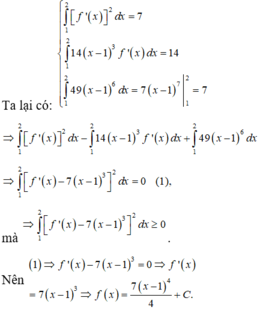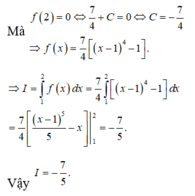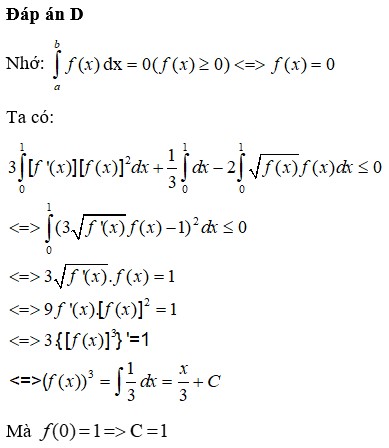Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

Đáp án A
Ta có - 1 30 = ∫ 1 2 x - 1 f ( x ) d x = 1 2 ∫ 1 2 f ( x ) d x - 1 2
= 1 2 x - 1 2 f ( x ) 1 2 - 1 2 ∫ 1 2 x - 1 2 f ' x d x
⇔ ∫ 1 2 x - 1 2 f ' ( x ) d x = 1 15
Ta lại có ∫ 1 2 x - 1 4 d x = 1 5 x - 1 5 1 2 = 1 5
Từ giả thiết và các kết quả ta có
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = 0
Mặt khác:
9 ∫ 1 2 f ' ( x ) 2 d x - 6 ∫ 1 2 x - 1 2 f ' ( x ) d x + ∫ 1 2 x - 1 4 d x = ∫ 1 2 3 f ' ( x ) - x - 1 2 2
Do vậy xét trên đoạn [1;2] , ta có
3 f ' ( x ) - ( x - 1 ) 2 = 0 ⇔ f ' ( x ) = 1 3 x - 1 2 ⇒ f ( x ) = 1 9 x - 1 3 + c
Lại do f(2) = 0 nên C + 1 9 = 0 ⇔ C = - 1 9 ⇒ f ( x ) = 1 9 x - 1 3 - 1 9
Suy ra I = 1 9 ∫ 1 2 x - 1 3 - 1 d x = 1 36 x - 1 4 1 2 - 1 9 x - 1 1 2 = - 1 12