Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Dựa vào công thức ứng dụng tích phân để tính thể tích vật tròn xoay.
Cách giải: V =

Ta có công thức tính thể tích khối tròn xoay quay đồ thị hàm số y = f ( x ) quanh trục hoành, giới hạn bởi 2 đường thẳng x = a, x = b ( a > b ) là.
V = π ∫ a b f 2 x dx
Đáp án cần chọn là A

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đáp án B
Cách giải: Thể tích V của khối nón tròn xoay thu được khi cho hình phẳng (H) giới hạn bởi đồ thị của y = f (x), x = a, x = b (a<b) khi quay xung quanh trục Ox tính bằng công thức: V = π ∫ a b f 2 ( x ) dx
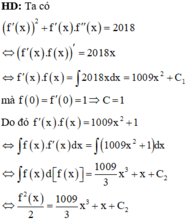

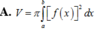
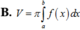
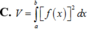
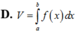

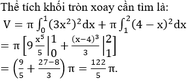
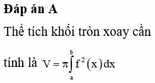
Chọn đáp án D.