Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

q chịu tác dụng của hai điện tích q 1 v à q 2 : → F → = F → 1 + F → 2
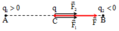
Do F → 1 ↑ ↑ F → 2 nên F = F 1 + F 2 = k q 1 q ε A C 2 + k q 2 q ε B C 2 = 2 , 25.10 − 4

đáp án A
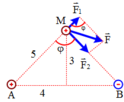
+ Các điện tích q1 và q2 tác dụng lên điện tích q các lực F1 và F2 có phương chiều như hình vẽ, có độ lớn lần lượt:
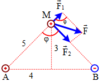
F 1 = k q 1 q r 2 = 9 . 10 9 . 10 - 8 . 10 - 8 0 , 05 2 = 3 , 6 . 10 - 4 N F 2 = k q 2 q r 2 = 9 . 10 9 . - 3 . 10 - 8 . 10 - 8 0 , 05 2 = 10 , 8 . 10 - 4 N
⇒ F = F 1 2 + F 2 2 - 2 F 1 F 2 cos φ → F = 12 , 3 . 10 - 4 N

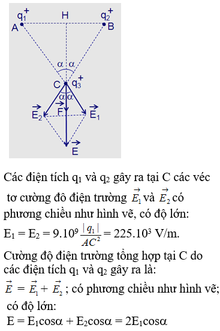
Tam giác ABC vuông tại C. Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường và có phương chiều như hình vẽ:
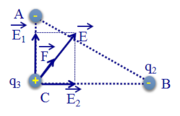
Có độ lớn: E 1 = 9 . 10 9 | q 1 | A C 2 = 255 . 10 4 V / m ; E 2 = 9 . 10 9 | q 2 | B C 2 = 600 . 10 4 V / m .
Cường độ điện trường tổng hợp tại C do q 1 v à q 2 gây ra là: E → = E 1 → + E 2 → ; có phương chiều như hình vẽ; có độ lớn: E = E 1 2 + E 2 2 ≈ 64 . 10 5 V/m.
Lực điện trường tổng hợp do q 1 v à q 3 tác dụng lên q 3 là: F → = q 3 E → . Vì q 3 > 0 , nên cùng phương cùng chiều với và có độ lớn: F = | q 3 |.E = 0,256 N.

a/
+ + A B + C q1 q2 q3 F F F 23 13 hl → → →
Ta có: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do \(\vec{F_{13}}\uparrow\downarrow\vec{F_{23}}\) nên: \(F_{hl}=\left|F_{13}-F_{23}\right|\) (1)
\(F_{13}=9.10^9\frac{\left|q_1q_2\right|}{AC^2}=0,045N\)
\(F_{23}=9.10^9\frac{\left|q_1q_2\right|}{BC^2}=0,01N\)
Thay vào (1) ta được \(F_{hl}=0,035N\)
b/
+ + + A B D q1 q2 q3 F F F 23 13 hl → → →
Hợp lực: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do hai lực cùng phương cùng chiều nên độ lớn:
\(F_{hl}=F_{13}+F_{23}\)(2)
\(F_{13}=9.10^9.\frac{\left|q_1q_3\right|}{AD^2}=7,2.10^{-3}N\)
\(F_{23}=9.10^9.\frac{\left|q_2q_3\right|}{BD^2}=0,9.10^{-3}N\)
Thế vào (2) ta được \(F_{hl}=8,1.10^{-3}N\)

Đáp án A
Các điện tích q 1 và q 2 tác dụng lên điện tích q các lực F → 1 và F → 2 có phương chiều như hình vẽ, có độ lớn lần lượt:
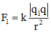
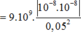
![]()
![]()
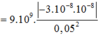
![]()
![]()
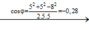
![]()


q chịu tác dụng của hai điện tích q 1 v à q 2 : F → = F → 1 + F → 2
Do F → 1 ↑ ↓ F → 2 nên F = F 1 − F 2 = k q 1 q ε A C 2 − k q 2 q ε B C 2 = 0