Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

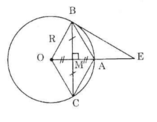
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều = > ∠ A O B = 60 °
Trong tam giác OBE vuông tại B ta có:
B E = O B . t g ∠ A O B = O B . t g 60 ° = R . √ 3

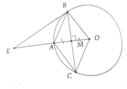
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3

a) Ta có OA⊥BC⇒MB=MC.
Mặt khác: MA=MO nên tứ giác ABOC là hình bình hành.
Hình bình hành này có hai đường chéo vuông góc nên là hình thoi. Vậy tứ giác ABOC là hình thoi
b) Ta có BA=BO (hai cạnh hình thoi)
mà BO=OA (bán kính) nên tam giác ABO là tam giác đều.
Suy ra góc BOA=60∘
Ta có EB là tiếp tuyến ⇒EB⊥OB.
Xét tam giác BOE vuông tại B, có:
BE=BO⋅tg60∘=R.tg600=R√3.
Created by potrace 1.16, written by Peter Selinger 2001-2019

a: ΔOBC cân tại O
mà OM là đường cao
nên M là trung điểm của BC
Xét tứ giác OCAB có
M là trung điểm chung của OA và BC
nên OCAB là hình bình hành
Hình bình hành OCAB có OB=OC
nên OCAB là hình thoi
b: Xét ΔOBA có OB=OA=AB
nên ΔOBA đều
=>\(\widehat{BOA}=60^0\)
Xét ΔOBE vuông tại B có \(tanBOE=\dfrac{BE}{BO}\)
=>\(\dfrac{BE}{R}=tan60=\sqrt{3}\)
=>\(BE=R\sqrt{3}\)

R B O C M A E
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA ( gt )
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA \(\perp\) BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => \(\Delta AOB\)đều => ∠AOB = 60o
Trong tam giác OBE vuông tại B ta có:
BE = OB . tg∠AOB = OB . tg60o = \(R.\sqrt{3}\)

a) Ta có : OA vuông góc BC tại M => M là trung điểm của BC
Mà M đồng thời là trung điểm của OA
=> Tứ giác OCAB là hình bình hành (do có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Lại có : OA vuông góc BC
=> OCAB là hình thoi ( do là hình bình hành có hai đường chéo vuông góc với nhau)
hoặc
ta có OC=OB=R (1)
dây BC vuông góc với OA tại trung điểm M của OA
=> OB=AB ( T/c tam giác cân ) (2)
=> OC=AC ( T/c tam giác cân ) (3)
từ (1);(2);(3) => OB=AB=AC=OC hay Tứ giác OCAB là hình thoi
b) ta có OB=AB=OA (cmt) => tam giác OBA đều
=>góc BAO = góc AOB = 60 độ => góc BAE = 120 đọ ( 2 góc kề bù )
xét tam giác OBE có góc AOB = 60 độ ; góc OBE = 90 độ ( t/c tiếp tuyến )
=>góc BEA = 30 độ
xét tam giác ABE có góc BEA = 30 độ ; góc BAE = 120 độ
=> góc ABE = 30 độ => tam giác ABE cân tại A ( góc BEA=ABE=30 độ )
=>BA=AE
mà BA=OA=R (cmt)
=>AE=R
ta có OE=OA+AE=R+R=2R
áp dụng định lý Py-Ta-Go trong tam giác vuông OBE ta có
OE^2=OB^2+BE^2
<=>(2R)^2=R^2+BE^2
<=>4R^2-R^2=BE^2
<=>BE^2=3R^2
hay BÉ = R căn 3.
học tốt
a) Xét \(\Delta\)ABM và \(\Delta\)OBM: AM=OM; AMB=OMB=90; BM chung
Do đó: \(\Delta\)ABM=\(\Delta\)OBM (c-g-c) =>AB=BO
Xét \(\Delta\)ABM và \(\Delta\)OCM: AB=OC(=OB);AMB=OMC=90; AM=OM
Do vậy: \(\Delta\)ABM=\(\Delta\)OCM (cạnh huyền - cạnh góc vuông)=>BM=CM, ABM=OCM=>BM=CM, AB//CO
Xét tứ giác ABCO có AB=CO,AB//CO, AO vuông góc với BC
Thế nên tứ giác ABCO là hình thoi
b) Xét tam giác vuông OBE có AB=AO(=R)
=> A là trung điểm OE
=>OE=2AO
Theo định lý Pythagore, ta có:
BE2=OE2-OB2
<=>BE2=4AO2-AO2=3AO2
=> BE=\(\sqrt{3}\)R
Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.