Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

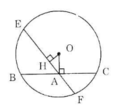
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

Vẽ OH⊥EFOH⊥EF.
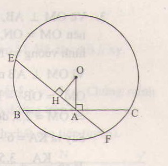
Xét tam giác HOA vuông tại H ta có OH<OA
Suy ra EF>BC..
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

giải:
Vẽ OH⊥EFOH⊥EF.
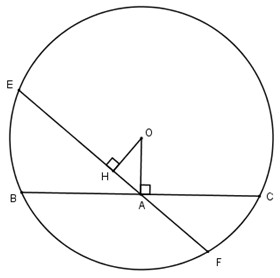
Xét tam giác HOA vuông tại H ta có:
OH<OAOH<OA.
Suy ra EF>BC.EF>BC.
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

b: \(AB=3\sqrt{3}\left(cm\right)\)
Xét ΔOAB vuông tại B có
\(\sin\widehat{AOB}=\dfrac{AB}{AO}=\dfrac{3\sqrt{3}}{6}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{AOB}=60^0\)

Lời giải:
Đề bài cần bổ sung OA cắt (O) tại E sao cho E nằm giữa O và A.
Do $AB$ là tiếp tuyến $(O)$ nên $AB\perp OB$ hay tam giác $ABO$ vuông tại $B$. Mà $AB=2BO$ (do $AB=2R; BO=R$). Do đó $\widehat{BOA}=60^0$
Tam giác $BOE$ có $BO=EO=R$ nên là tam giác cân. Mà $\widehat{BOE}=\widehat{BOA}=60^0$ nên $BOE$ là tam giác đều.
$\Rightarrow BO=BE(1)$$OB=OC$ và $OA\perp BC$ nên $OA$ là đường trung trực của $BC$
$E\in OA$ nên $EB=EC(2)$
$OB=OC=R(3)$
Từ $(1);(2);(3)\Rightarrow OC=BO=BE=EC$. Suy ra OBEC là hình thoi.

Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).