Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số mol C = 0,05 mol; số mol O = 0,08 mol.
Gọi số mol CO là x; CO2 là y;
x + y = 0,05 và x + 2y = 0,08
x = 0,02; y = 0,03
x/y = 2/3

Câu 4
Gọi x là số mol Fe3O4; 3x là số mol CuO. Ta có: 80.3x + 232x = 4,72 thu được x = 0,01 mol.
Số mol CO và H2 = nO = nCuO + 4nFe3O4 = 0,03 + 0,04 = 0,07 mol. V = 1.568 lít.
Vì sao mà có được như vậy giải thích rõ hơn được không ạ
Số mol CO và H2 = nO = nCuO + 4nFe3O4 = 0,03 + 0,04 = 0,07 mol. V = 1.568 lít.

Đáp án B
nCO2 = 0,9 mol => nC = 0,9 mol
nH2O = 0,975 mol => nH = 1,95 mol
nH2O>nCO2 => Ancol no
Ctb = 0,9/0,325 = 2,77
Do Z đa chức và có M>90 => Z có số C ≥ 3
=> 2 ancol chỉ có thể là C2H5OH và C2H4(OH)2
=> Z là axit no, 3 chức, mạch hở: CnH2n-4O6
=> T là este no, 3 chức, 1 vòng: Cn+4H2n+2O6
Htb = 1,95/0,325 = 6
Do este có số H>6 nên axit phải có H<6
Vậy E gồm:
X: C2H6O (x mol)
Y: C2H6O2 (y mol)
Z: C4H4O6 (z mol)
T: C8H10O6 (t mol)
x+y+z+t = 0,325
BTNT C: 2x+2y+4z+8t = 0,9
BTNT H: 6x+6y+4z+10t = 1,95
Giải ta thu được: x+y = 0,25; z = 0,05; t = 0,025
%nT = 0,025/0,325 = 7,7%

a) Ta có: Mật độ xác suất tìm thấy electron trong vùng không gian xung quanh hạt nhân nguyên tử:
D(r) = R2(r) . r2
= 416/729 . a0-5 . r2 . (2 - r/3a0)2 . e-2r/3a0 . r2
= 416/729 . a0-5 . (4r4 - 4r5/3a0 + r6/9a02) . e-2r/3a0
Khảo sát hàm số D(r) thuộc r
Xét: d D(r)/ dr = 416/729 . a0-5 . [(16r3 - 20r4/3a0 + 2r5/3a02) . e-2r/3a0 - (4r4 - 4r5/3a0 + r6/9a02) . 2/3a0 . e-2r/3a0 ]
= 416/729 . a0-5 . e-2r/3a0 . r3 . (16a03 - 28r/3a0 + 14r2/9a02 - 2r3/27a03)
= 832/19683 . a0-8 . e-2r/3a0 . r3 . (-r3 +21r2.a0 - 126r.a02 +216a03)
= - 832/19683 . a0-8 . e-2r/3a0 . r3 . (r - 6a0).(r - 3a0).(r - 12a0)
d D(r)/ dr = 0. Suy ra r =0; r =3a0 ; r = 6a0; r = 12a0
Với r = 0 : D(r) =0
r =3a0 : D(r) = 416/9 .a-1 . e-2
r =6a0 : D(r) = 0
r =12a0 : D(r) = 425984/9.a-1 . e-8
b) Ai vẽ câu này rồi cho up lên với, cám ơn mọi người trước nhé!
a)Mật độ xác suất có mặt electron tỷ lệ với |R3P|2.r2
D(r)=|R3P|2.r2 =D (r)=\(\frac{416}{729}\) .a0-5.(2r2- \(\frac{r^3}{3a_0}\)).\(^{e^{-\frac{2r}{3a_0}}}\)
Lấy đạo hàm của D theo r để khảo sát mật độ xác suất :
D' (r)= \(\frac{416}{729}\) .a0-5.2.(2r2-\(\frac{r^3}{3a_0}\)).(4r-\(\frac{r^2}{a_0}\)).\(^{e^{-\frac{2r}{3a_0}}}\)+\(\frac{416}{729}\) .a0-5.(2r2-\(\frac{r^3}{3a_0}\))2.(-\(\frac{2}{3a_0}\)).\(^{e^{-\frac{2r}{3a_0}}}\)
=\(\frac{832}{729}\). a0-6.\(^{e^{-\frac{2r}{3a_0}}}\). (2r2-\(\frac{r^3}{3a_0}\)) .[(4r-\(\frac{r^2}{a_0}\)).a0 -\(\frac{1}{3}\). (2r2-\(\frac{r^3}{3a_0}\))]
=\(\frac{832}{729}\). a0-6.\(^{e^{-\frac{2r}{3a_0}}}\).r3.(2- \(\frac{r}{3a_0}\)).(\(\frac{r^2}{9a_0}-\frac{5r}{3}+4a_0\))
=>D’(r)=0 => r=0 ,r=3a0 ,r=6a0 ,r=12a0.
Với:r=0 =>D(r)=0
r=3a0 =>D(r)=0
r=6a0 =>D(r)=\(\frac{416}{9a_0.e^2}\)
r=12a0=>D(r)=\(\frac{425984}{a_0.e^8}\)
b)

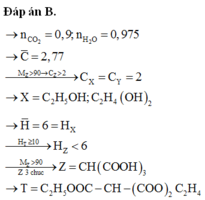
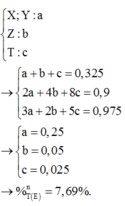
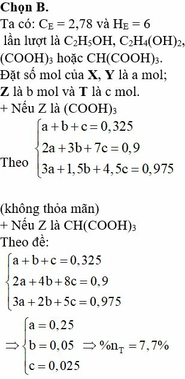
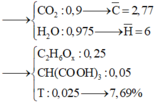
Đáp án B