Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

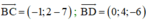
(BCD) nhận 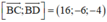 là 1 vtpt
là 1 vtpt
⇒ (BCD): 16x – 6y – 4z + 8 = 0
hay (BCD): 8x – 3y – 2z + 4 = 0.

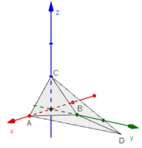
a) Cách 1:
Phương trình đoạn chắn (ABC) là:
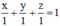 hay x + y + z – 1 = 0.
hay x + y + z – 1 = 0.
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0
⇒ D không nằm trong (ABC)
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của một tứ diện.
Cách 2:
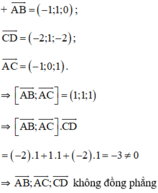
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của hình tứ diện.

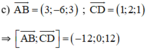
(α) chứa AB và song song với CD
⇒ (α) nhận (1; 0; -1) là 1 vtpt
(α) đi qua A(-2; 6; 3)
⇒ (α): x – z + 5 = 0.

Mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC) nên ( α ) cũng có vecto pháp tuyến là n ' → = (1; 1; 1)
Vậy phương trình của ( α ) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.

Chọn B
Mặt phẳng (ABC) đi qua B (1; 0; -1) và có một véctơ pháp tuyến là:
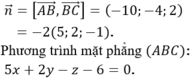
Phương trình mặt phẳng (ABC): 5x + 2y - z - 6 = 0
Độ dài đường cao xuất phát từ đỉnh D (0; 0; d) của tứ diện ABCD bằng d(D, (ABC))
Theo bài ra ta có:
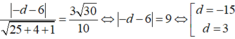
Do D thuộc tia Oz nên D (0; 0; 3).

Vecto pháp tuyến của mặt phẳng (ACD) vuông góc với hai vecto A C → = 0 ; - 1 ; 1 v à A D → = - 1 ; - 1 ; 3


Ta có: AB → = (−4; 5; −1) và AC → = (0; −1; 1) suy ra n → = AB → ∧ n → = (4; 4; 4)
Do đó (ABC) có vecto pháp tuyến là n → = (4; 4; 4) hoặc n ' → = (1; 1; 1)
Suy ra phương trình của (ABC) là: (x – 5) + (y – 1) + (z – 3) = 0 hay x + y + z – 9 =0

Độ dài đường cao hình chóp A.BCD chính là khoảng cách từ A đến (BCD).
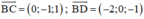
⇒ (BCD) nhận 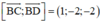 là 1 vtpt
là 1 vtpt
⇒ (BCD): x – 2y – 2z + 2 = 0
⇒ Độ dài đường cao hình chóp A.BCD là:
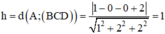

Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mp (BCD) :