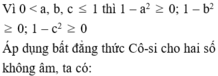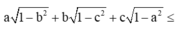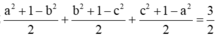Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(m=a^2+b^2+c^2,m\ge0\)
Áp dụng bất đẳng thức Bunhiacopxki , ta có :
\(\frac{9}{4}=\left(a.\sqrt{1-b^2}+b.\sqrt{1-c^2}+c.\sqrt{1-a^2}\right)^2\le\left(a^2+b^2+c^2\right)\left(3-a^2-b^2-c^2\right)\)
\(\Rightarrow m\left(3-m\right)\ge\frac{9}{4}\) \(\Leftrightarrow\left(m-\frac{3}{2}\right)^2\le0\) mà ta luôn có \(\left(m-\frac{3}{2}\right)^2\ge0\)
Do đó \(\left(m-\frac{3}{2}\right)^2=0\Rightarrow m=\frac{3}{2}\)
Vậy \(a^2+b^2+c^2=\frac{3}{2}\)

Đặt \(x=a^2+b^2+c^2\), cần chứng minh \(x=\frac{3}{2}\)
Từ giả thiết \(a\sqrt{1-b^2}+b\sqrt{1-a^2}+c\sqrt{1-a^2}=\frac{3}{2}\) , áp dụng bất đẳng thức Bunhiacopxki , ta có :
\(\left(\frac{3}{2}\right)^2=\left(a.\sqrt{1-b^2}+b.\sqrt{1-c^2}+c.\sqrt{1-a^2}\right)^2\)
\(\le\left(a^2+b^2+c^2\right)\left[3-a^2-b^2-c^2\right]\)
\(\Rightarrow x\left(3-x\right)\ge\frac{9}{4}\Leftrightarrow x^2-3x+\frac{9}{4}\le0\Leftrightarrow\left(x-\frac{3}{2}\right)^2\le0\)(1)
Mà ta luôn có \(\left(x-\frac{3}{2}\right)^2\ge0\) (2)
Từ (1) và (2) suy ra \(\left(x-\frac{3}{2}\right)^2=0\Leftrightarrow x=\frac{3}{2}\)
Vậy \(a^2+b^2+c^2=\frac{3}{2}\)(đpcm)

Áp dụng BĐT côsi ta có:
\(VT\le\frac{a^2+1-b^2}{2}+\frac{b^2+1-c^2}{2}+\frac{c^2+1-a^2}{2}=\frac{3}{2}\)
Đẳng thức đề bài chỉ xảy ra khi \(a=b=c=\frac{\sqrt{2}}{2}\)
=> \(a^2+b^2+c^2=\frac{3}{2}\)(ĐPCM)

Ta có:
\(\frac{a+1}{1+b^2}=a+1-\frac{\left(a+1\right)b^2}{1+b^2}\ge a+1-\frac{\left(a+1\right)b^2}{2b}=a+1-\frac{ab+b}{2}\left(1\right)\)
Tương tụ ta có:
\(\hept{\begin{cases}\frac{\left(b+1\right)}{1+c^2}\ge b+1-\frac{bc+c}{2}\left(2\right)\\\frac{\left(c+1\right)}{1+a^2}\ge c+1-\frac{ca+a}{2}\left(3\right)\end{cases}}\)
Từ (1), (2), (3) ta có:
\(M\ge a+b+c+3-\frac{ab+bc+ca+a+b+c}{2}\)
\(=3+3-\frac{ab+bc+ca+3}{2}\)
\(\ge\frac{9}{2}-\frac{\left(a+b+c\right)^2}{6}=3\)

Bạn kia làm sai r
Ta có đánh giá quen thuộc \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=\frac{a+b+c}{abc}\)
mà \(3abc\left(a+b+c\right)\le\left(ab+bc+ca\right)^2\)
do đó \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{a+b+c}{abc}=\frac{\left(a+b+c\right)^2}{abc\left(a+b+c\right)}\ge\frac{3\left(a+b+c\right)^2}{\left(ab+bc+ca\right)^2}\)
Phép chứng minh hoàn tất khi ta cm được
\(\frac{3\left(a+b+c\right)^2}{\left(ab+bc+ca\right)^2}\ge a^2+b^2+c^2\)
hay \(3\left(a+b+c\right)^2\ge\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)^2\)
Theo bđt AM-GM ta có
\(\left(a+b+c\right)^2=\left(a^2+b^2+c^2\right)+\left(ab+bc+ca\right)+\left(ab+bc+ca\right)\)
\(\ge3\sqrt[3]{\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)^2}\)
hay \(\left(a+b+c\right)^6\ge27\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)^2\)
mà a+b+c=3 nên \(\left(a+b+c\right)^6=81\left(a+b+c\right)^2\)
\(\Rightarrow3\left(a+b+c\right)^2\ge\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)^2\)
Vậy bđt được chứng minh
Dấu "=" xảy ra khi a=b=c=1
Xét BĐT phụ \(\frac{1}{a^2}+4a\ge a^2+4\Leftrightarrow\frac{\left(a-1\right)^2\left(1+2a-a^2\right)}{a^2}\ge0\)
Đến đây, ta đưa điều phải chứng minh về dạng \(\frac{\left(a-1\right)^2\left(1+2a-a^2\right)}{a^2}+\frac{\left(b-1\right)^2\left(1+2b-b^2\right)}{b^2}+\frac{\left(c-1\right)^2\left(1+2c-c^2\right)}{c^2}\ge0\)(*)
Không mất tính tổng quát, giả sử \(a\ge b\ge c\)
Xét hai trường hợp:
Trường hợp 1: \(a\le1+\sqrt{2}\Rightarrow c\le b\le a\le1+\sqrt{2}\)
Khi đó thì \(1+2a-a^2\ge0;1+2b-b^2\ge0;1+2c-c^2\ge0\)dẫn đến (*) đúng
Trường hợp 2: \(a>1+\sqrt{2}\Rightarrow b+c=3-a< 3-\left(1+\sqrt{2}\right)=2-\sqrt{2}< \frac{2}{3}\)
\(\Rightarrow bc\le\frac{\left(b+c\right)^2}{4}< \frac{\frac{4}{9}}{4}=\frac{1}{9}\)
Mà a,b,c dương nên \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}>\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}>18>\left(a+b+c\right)^2>a^2+b^2+c^2\)
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi a = b = c = 1

1.Ta có: \(c+ab=\left(a+b+c\right)c+ab\)
\(=ac+bc+c^2+ab\)
\(=a\left(b+c\right)+c\left(b+c\right)\)
\(=\left(b+c\right)\left(a+b\right)\)
CMTT \(a+bc=\left(c+a\right)\left(b+c\right)\)
\(b+ca=\left(b+c\right)\left(a+b\right)\)
Từ đó \(P=\sqrt{\frac{ab}{\left(a+b\right)\left(b+c\right)}}+\sqrt{\frac{bc}{\left(c+a\right)\left(a+b\right)}}+\sqrt{\frac{ca}{\left(b+c\right)\left(a+b\right)}}\)
Ta có: \(\sqrt{\frac{ab}{\left(a+b\right)\left(b+c\right)}}\le\frac{1}{2}\left(\frac{a}{a+b}+\frac{b}{b+c}\right)\)( theo BĐT AM-GM)
CMTT\(\Rightarrow P\le\frac{1}{2}\left(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{a+c}+\frac{b}{a+b}+\frac{c}{b+c}+\frac{a}{a+b}\right)\)
\(\Rightarrow P\le\frac{1}{2}.3\)
\(\Rightarrow P\le\frac{3}{2}\)
Dấu"="xảy ra \(\Leftrightarrow a=b=c\)
Vậy /...
\(\frac{a+1}{b^2+1}=a+1-\frac{ab^2-b^2}{b^2+1}=a+1-\frac{b^2\left(a+1\right)}{b^2+1}\ge a+1-\frac{b^2\left(a+1\right)}{2b}\)
\(=a+1-\frac{b\left(a+1\right)}{2}=a+1-\frac{ab+b}{2}\)
Tương tự rồi cộng lại:
\(RHS\ge a+b+c+3-\frac{ab+bc+ca+a+b+c}{2}\)
\(\ge a+b+c+3-\frac{\frac{\left(a+b+c\right)^2}{3}+a+b+c}{2}=3\)
Dấu "=" xảy ra tại \(a=b=c=1\)

2/
- Chứng minh \(\sqrt{2}\left(a+b+c\right)\le\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\)
Ta có \(\sqrt{2}.\left(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\right)\ge2\left(a+b+c\right)\)
\(\Leftrightarrow\sqrt{2}\left(a+b+c\right)\le\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\)
- Chứng minh \(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}< \sqrt{3}\left(a+b+c\right)\)
Bạn chứng minh bằng biến đổi tương đương
1/ \(ab+bc+ac=3abc\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\)
Ta có \(\frac{1}{a^2+1}+\frac{1}{b^2+1}+\frac{1}{c^2+1}\le\frac{1}{2a}+\frac{1}{2b}+\frac{1}{2c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{3}{2}\)
Vậy min P = 3/2 tại a = b = c = 1

Dễ thấy các hệ số tương đồng nhau nên có thể biến đổi bđt về dạng sau :
\(\left(\frac{1}{a^2}+\frac{2a^2}{3}\right)+\left(\frac{1}{b^2}+\frac{2b^2}{3}\right)+\left(\frac{1}{c^2}+\frac{2c^2}{3}\right)\ge5\)
Ta đi chứng minh bđt phụ sau : \(\frac{1}{a^2}+\frac{2a^2}{3}\ge\frac{7}{3}-\frac{2a}{3}\)(1)
\(Bđt\left(1\right)\Leftrightarrow\frac{1}{a^2}+\frac{2a^2}{3}-\frac{7}{3}+\frac{2a}{3}\ge0\)
\(\Leftrightarrow\frac{3+2a^4-7a^2+2a^3}{3a^2}\ge0\)
\(\Leftrightarrow\frac{2\left(a^4-2a^2+1\right)+2a^3-3a^2+1}{3a^2}\ge0\)
\(\Leftrightarrow\frac{2\left(a^2-1\right)^2+2a^2\left(a-1\right)-\left(a^2-1\right)}{3a^2}\ge0\)
\(\Leftrightarrow\frac{2\left(a-1\right)^2\left(a+1\right)^2+2a^2\left(a-1\right)-\left(a-1\right)\left(a+1\right)}{3a^2}\ge0\)
\(\Leftrightarrow\frac{\left(a-1\right)\left[2\left(a-1\right)\left(a+1\right)^2+2a^2-a-1\right]}{3a^2}\ge0\)
\(\Leftrightarrow\frac{\left(a-1\right)\left[2\left(a-1\right)\left(a+1\right)^2+\left(a-1\right)\left(2a+1\right)\right]}{3a^2}\ge0\)
\(\Leftrightarrow\frac{\left(a-1\right)^2\left[2\left(a+1\right)^2+2a+1\right]}{3a^2}\ge0\)(Luôn đúng do a > 0 nên [...] > 0)
Dấu "=" <=> a = 1
Thiết lập các bđt còn lại \(\frac{1}{b^2}+\frac{2b^2}{3}\ge\frac{7}{3}-\frac{2b}{3}\)
\(\frac{1}{c^2}+\frac{2c^2}{3}\ge\frac{7}{3}-\frac{2c}{3}\)
Cộng 3 vế của bdtd lại ta được
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2\left(a^2+b^2+c^2\right)}{3}\ge7-\frac{2\left(a+b+c\right)}{3}=7-\frac{2.3}{3}=5\)
Dấu "=" xảy ra khi a = b = c = 1