
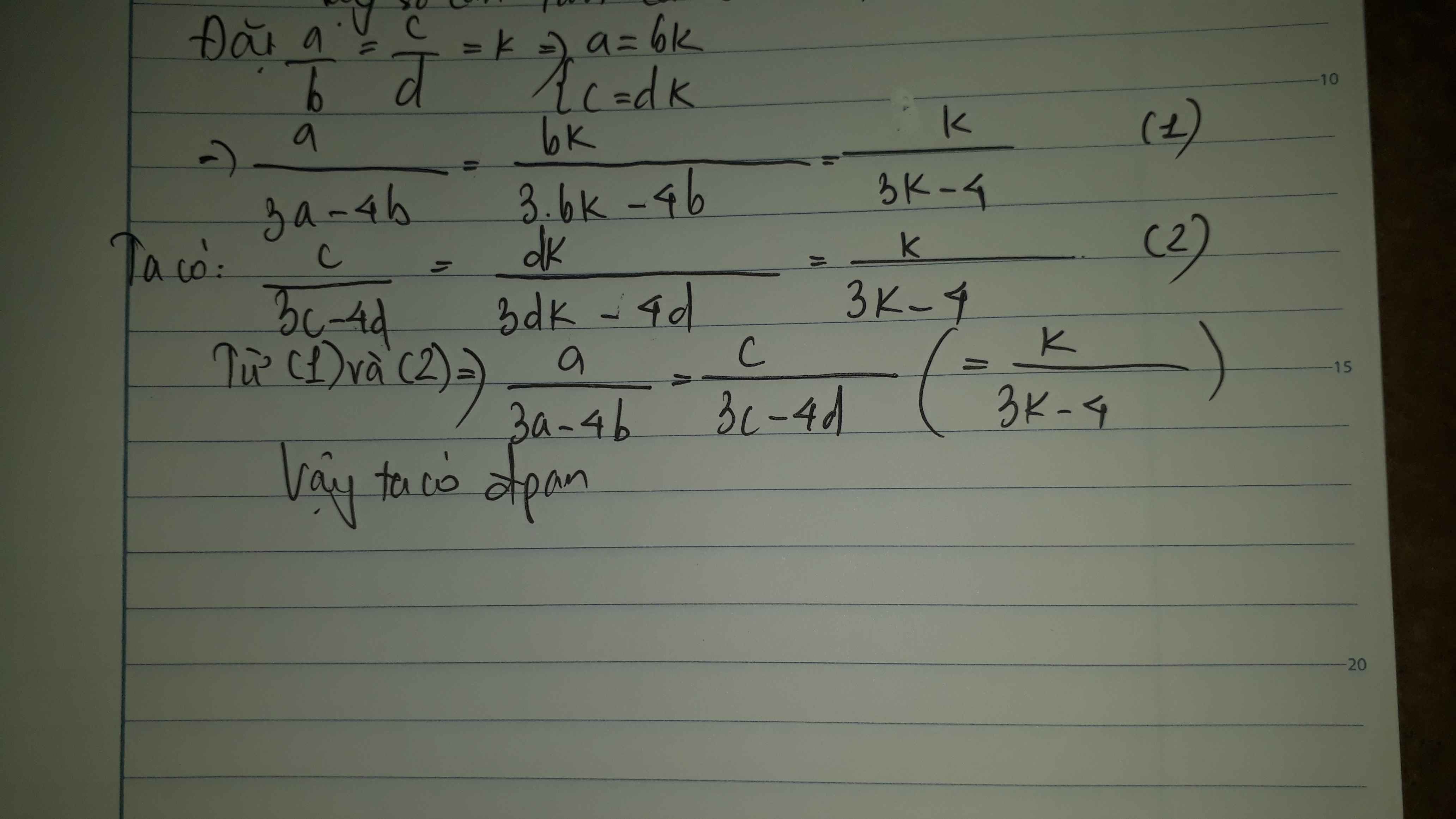
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

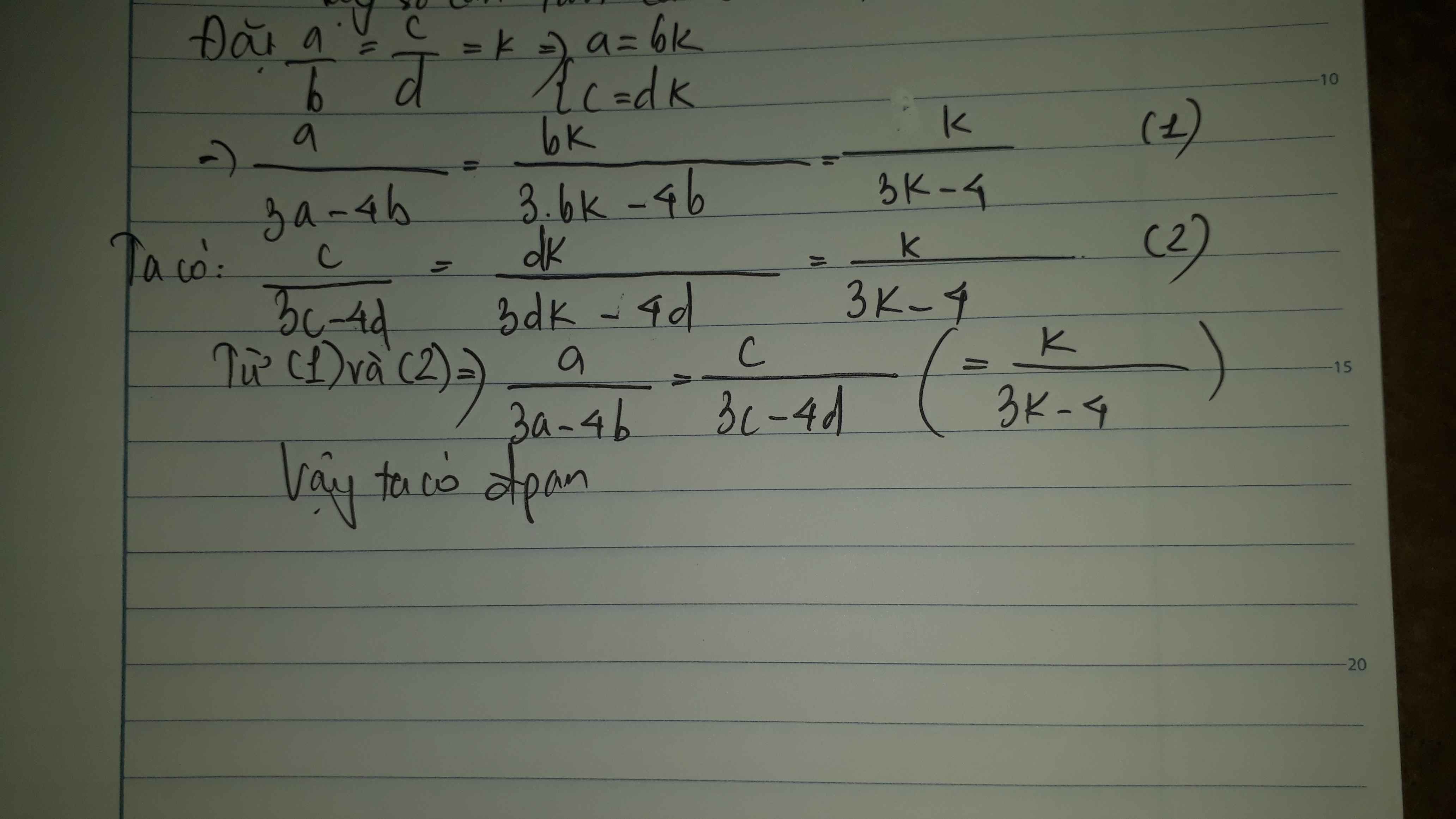

Ta có: \(\frac{3a+4b}{3a-4b}=\frac{3c+4d}{3c-4d}\)
\(\Rightarrow\frac{3a+4b}{3a-4b}-1=\frac{3c+4d}{3c-4d}-1\)
\(\Leftrightarrow\frac{8b}{3a-4b}=\frac{8d}{3c-4d}\)
\(\Rightarrow b\left(3c-4d\right)=d\left(3a-4b\right)\)
\(\Leftrightarrow3bc=3ad\)
\(\Rightarrow\frac{a}{b}=\frac{c}{d}\left(đpcm\right)\)

Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Lại có :
\(VT=\dfrac{2a+5b}{3a-4b}=\dfrac{2bk+5b}{3bk-4b}=\dfrac{b\left(2k+5\right)}{b\left(3k-4\right)}=\dfrac{2k+5}{3k-4}\left(1\right)\)
\(VP=\dfrac{2c+5d}{3c-4d}=\dfrac{2dk+5d}{3dk-4d}=\dfrac{d\left(2k+5\right)}{d\left(3k-4\right)}=\dfrac{2k+5}{3k-4}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
Theo đề ta có:
\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
=> \(\dfrac{2a+5b}{3a-4b}-\dfrac{2c+5d}{3c-4d}\)
=> \(\dfrac{a+b}{a-b}-\dfrac{c+d}{c-d}\)(1)
Mà \(\dfrac{a}{b}=\dfrac{c}{d}\)
=> \(\dfrac{a}{c}=\dfrac{b}{d}\)(2)
=> \(\dfrac{a-b}{c-d}\) và \(\dfrac{a+b}{c+d}\)(3)
Từ (2) và (3) => \(\dfrac{a-b}{c-d}\) = \(\dfrac{a+b}{c+d}\) = \(\dfrac{a}{b}=\dfrac{c}{d}\)
=> \(\dfrac{a-b}{c-d}\) = \(\dfrac{a+b}{c+d}\)= > \(\dfrac{a-b}{a+b}\) = \(\dfrac{c-d}{c+d}\)
=> \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)= \(\dfrac{a+b}{a-b}-\dfrac{c+d}{c-d}\)(4)
Từ (1) và (4)
=> \(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)( đpcm)

Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{3c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\)
\(\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\) (đpcm)
Chúc bạn học tốt nha![]()
Điều kiện nào mà bạn chứng minh được như đề bài yêu cầu đc?
3a - 4b có khác 0 không?
cậu lý ở đâu ra đấy?
Lý luận đâu?

Đặt \(\frac{a}{b}=\frac{c}{d}=v\)
\(\Rightarrow\hept{\begin{cases}a=vb\\c=vd\end{cases}}\)( 1 )
Thay (1) vào vế trái , ta có :
\(VT=\frac{2vb+5b}{3vb-4b}=\frac{b\left(2v+5\right)}{b\left(3v-4\right)}=\frac{2v+5}{3v-4}\)( *)
Thay (1) vào vế phải ta có :
\(VP=\frac{2vd+5d}{3vd-4d}=\frac{2v+5}{3v-4}\)(**)
Từ ( * ) và (** )
=> ĐPCM

\(\frac{a}{b}=\frac{c}{d}\Rightarrow\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
\(\frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b\left(2k+5\right)}{b\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{d\left(2k+5\right)}{d\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\Rightarrow\frac{2a+5b}{3a-4b}=\frac{2a+5d}{3c-4d}\)
Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}-\frac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{2a}{2c}=\frac{5b}{5d}=\frac{2a+5b}{2c+5d}\)
\(\frac{a}{c}=\frac{b}{d}=\frac{3a}{3c}=\frac{4b}{4d}=\frac{3a-4b}{3c-4d}\)
\(\Rightarrow\frac{2a+5b}{2c+5d}=\frac{3a-4d}{3c-4d}\left(=\frac{a}{c}\right)\)
\(\Rightarrow\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\left(đpcm\right)\)

Từ \(\frac{a}{b}=\frac{c}{d}=>\frac{a}{c}=\frac{b}{d}=\frac{3a}{3c}=\frac{4b}{4d}\)
Aps dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{3a}{3c}=\frac{4b}{4d}=\frac{3a+4b}{3c+4d}\)
=>\(\frac{a}{c}=\frac{3a+4b}{3c+4d}=>\frac{3c+4d}{c}=\frac{3a+4b}{a}\)(đpcm)
a/b=c/d
=>a/c=b/d=3a/3c=4b/4d=(3a+4b)/(3c+4d) (tính chất dãy tỉ số = nhau)
có a/c=(3a+4b)/(3c+4d)
=>dpcm

a) ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\frac{3a}{3c}=\frac{4b}{4d}=\frac{3a+4b}{3c+4d}=\frac{3a-4b}{3c-4d}.\)
\(\Rightarrow\frac{3a+4b}{3a-4b}=\frac{3c+4d}{3c-4d}\)
b) ta có: \(\frac{a}{b}=\frac{c}{d}=\frac{5a}{5b}=\frac{2c}{2d}=\frac{4a}{4b}\)
Lại có: \(\frac{5a}{5b}=\frac{2c}{2d}=\frac{5a+2c}{5b+2d}\)
\(\Rightarrow\frac{4a}{4b}=\frac{5a+2c}{5b+2d}\Rightarrow\frac{5a+2c}{4a}=\frac{5b+2d}{4b}\)
c) ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{\left(a+b\right)^2}{\left(c+d\right)^2}\)
Lại có: \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
\(\Rightarrow\frac{\left(a+b^2\right)}{\left(c+d\right)^2}=\frac{a^2+b^2}{c^2+d^2}\)

Đặt\(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
Khi đó: \(\frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b\left(2k+5\right)}{b\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{d\left(2k+5\right)}{d\left(3k-4\right)}=\frac{2k+5}{3k-4}\)
\(\Rightarrow\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\left(=\frac{2k+5}{3k-4}\right)\)
Từ\(\frac{a}{b}\)=\(\frac{c}{d}\)suy ra \(\frac{a}{c}\)=\(\frac{b}{d}\)( t/c TLT)
Áp dụng tính chất của dãy TSBN ta có:\(\frac{a}{c}\)=\(\frac{b}{d}\)=\(\frac{2a+5b}{2c+5d}\)=\(\frac{3a-4b}{3c-4d}\)
Từ \(\frac{2a+5b}{2c+5d}\)=\(\frac{3a-4b}{3c-4d}\) suy ra\(\frac{2a+5b}{3a-4b}\)=\(\frac{2c+5d}{3c-4d}\)(t/c TLT)

a/ Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có :
\(\dfrac{2a+7b}{3a-4b}=\dfrac{2bk+7b}{3bk-4b}=\dfrac{b\left(2k+7\right)}{b\left(3k-4\right)}=\dfrac{2k+7}{3k-4}\left(1\right)\)
\(\dfrac{2c+7d}{3c-4d}=\dfrac{2dk+7d}{3dk-4d}=\dfrac{d\left(2k+7\right)}{d\left(3k-4\right)}=\dfrac{2k+7}{3k-4}\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
b/ tương tự