Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B= \(\left[\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\right]^2\)
ta thấy : \(\left(x+\frac{1}{2}\right)^2\ge0\)
=> \(\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
=>\(\left[\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\right]^2\ge\frac{9}{16}\)
=> min B=9/16 kh x=-1/2
C= \(x^2-2xy+y^2+1\)= \(\left(x-y\right)^2+1\)
ta có \(\left(x-y\right)^2\ge0\)=>\(\left(x-y\right)^2+1\ge1\)
=> Min C=1 khi x=y

a) \(16x^2-\left(4x-5\right)^2=15\) \(\Leftrightarrow\) \(16x^2-\left(16x^2-40x+25\right)=15\)
\(\Leftrightarrow\) \(16x^2-16x^2+40x-25=15\) \(\Leftrightarrow\) \(40x-25=15\)
\(\Leftrightarrow\) \(40x=40\) \(\Leftrightarrow\) \(x=1\) vậy \(x=1\)
b) \(\left(2x+3\right)^2-4\left(x-1\right)\left(x+1\right)=49\)
\(\Leftrightarrow\) \(4x^2+12x+9-4\left(x^2-1\right)=49\)
\(\Leftrightarrow\) \(4x^2+12x+9-4x^2+4=49\)
\(\Leftrightarrow\) \(12x+13=49\) \(\Leftrightarrow\) \(12x=36\) \(\Leftrightarrow\) \(x=\dfrac{36}{12}=3\)vậy \(x=3\)
c) \(\left(2x+1\right)\left(2x-1\right)+\left(1-2x\right)^2=18\)
\(\Leftrightarrow\) \(4x^2-1+1-4x+4x^2=18\)\(\Leftrightarrow\) \(8x^2-4x=18\)
\(\Leftrightarrow\) \(8x^2-4x-18=0\)
\(\Delta'=\left(-2\right)^2-8.\left(-18\right)=4+144=148>0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{2+\sqrt{148}}{8}=\dfrac{1+\sqrt{37}}{4}\)
\(x_2=\dfrac{2-\sqrt{148}}{8}=\dfrac{1-\sqrt{37}}{4}\)
vậy \(x=\dfrac{1+\sqrt{37}}{4};x=\dfrac{1-\sqrt{37}}{4}\)
Giải:
a) \(16x^2-\left(4x-5\right)^2=15\)
\(\Leftrightarrow16x^2-16x^2-40x+25=15\)
\(\Leftrightarrow-40x+25=15\)
\(\Leftrightarrow-40x=15-25=-10\)
\(\Leftrightarrow x=-\dfrac{10}{-40}=\dfrac{1}{4}\)
Vậy \(x=\dfrac{1}{4}\)
b) \(\left(2x+3\right)^2-4\left(x-1\right)\left(x+1\right)=49\)
\(\Leftrightarrow4x^2+12x+9-4\left(x^2-1^2\right)=49\)
\(\Leftrightarrow4x^2+12x+9-4x^2+4=49\)
\(\Leftrightarrow12x+9+4=49\)
\(\Leftrightarrow12x=49-9-4\)
\(\Leftrightarrow12x=36\)
\(\Leftrightarrow x=\dfrac{36}{12}=3\)
Vậy \(x=3\)
c) \(\left(2x+1\right)\left(2x-1\right)+\left(1-2x\right)^2=18\)
\(\Leftrightarrow4x^2-1+1-4x+4x^2=18\)
\(\Leftrightarrow8x^2-4x=18\)
Mình chỉ làm được đến đây thôi, hình như là đề bị sai bạn nhé!
Chúc bạn học tốt!

Số phần tử của tập hợp A = { k2 + 1 | k εℤ, |k| \(\le\)2} là:
A. 1
B. 2
C. 3
D. 5

a) Thay x= 1/2 và y=-1/3 vào biểu thức A, ta được:
A= 3.(1/2)2 .(-1/3)+ 6.(1/2).(-1/3)2+ 3.(1/2).(-1/3)3= -7/8
Vậy giá trị của biểu thức A tại x=1/2 và y=-1/3 là -7/8

a) ta có :(2^14:1024).2^x=128
=>(2^14:2^10).2^x=2^7
=>2^4.2^x=2^7
=>2^x=2^7:2^4
=>2^x=2^3
=>x=3
b) ta có: 3^x+3^x+1+3^x+2=117
=>3^x.(1+3+3^2)=117
=>3^x.13=117
=>3^x=9=3^2
=>x=2
c)ta có 2^x+2^x+1+2^x+2+2^x+3=480
=>2^x.(1+2+2^2+2^3)=480
=>2^x.15=480
=>2^x=480:15=32=2^5
=>x=5
d) ta có: 2^3.32>=2^n>16
=>2^3.2^5>=2^>2^4
=>2^8>=2^n>2^4
=>n=8;7;6;5
còn lại tương tự
h)16^n<32^4
=>(2^4)^n<(2^5)^4
=>2^4n<2^20
=>4n<20
=>n= 0;1;2;3;4

\(sina+cosa=\sqrt{2}\Leftrightarrow\left(sina+cosa\right)^2=2\\ \)
\(\Leftrightarrow\sin^2a+2\sin a.cosa+cos^2a=2\)
\(\Leftrightarrow1+2.sina.cosa=2\)
\(\Leftrightarrow2.sina.cosa=2-1=1\)
\(\Leftrightarrow\sin a.cosa=\frac{1}{2}\)
Vậy P=sina.cosa=\(\frac{1}{2}\)
\(Q=\sin^4a+cos^4a\)
\(\Leftrightarrow\left(sin^2a\right)^2+\left(cos^2a\right)^2\)
\(\Leftrightarrow\left(sin^2a+cos^2a\right)^2-2.sin^2a.cos^2a\)
\(\Leftrightarrow1^2-2.sin^2a.cos^2a\) tách tiếp rồi thế vào là được .tương tự phàn P ý
còn R thì tách sin^3a=sin^2a+sina tương tự cos mũ 3 a cụng vậy
theo tớ là như thế còn có sai thì đừng có ném đá ném gạch na

Bài 1:
\(A=\left(1+sinx\right)\left(1-sinx\right)tan^2x=\left(1-sin^2x\right).\frac{sin^2x}{cos^2x}=cos^2x.\frac{sin^2x}{cos^2x}=cos^2x\)
\(B=cot^2x-sin^2x.cot^2x+1-cot^2x=1-sin^2x.\frac{cos^2x}{sin^2x}=1-cos^2x=sin^2x\)
\(C=tan^2x+2+\frac{1}{tan^2x}-\left(tan^2x-2+\frac{1}{tan^2x}\right)=2+2=4\)
Bài 2:
Đề yêu cầu tính giá trị lượng giác nào bạn? sin?cos?tan?cot?
Không hỏi thì làm sao mà biết cần tính gì

a) P = sin2α + sin2α.\(\frac{cos\text{α}}{sin\text{α}}\) + cos2α - cos2α.\(\frac{sin\text{α}}{cos\text{α}}\)
=sin2α + sinα.cosα + cos2α - cosα.sinα
=sin2α + cos2α
=1
Vậy P không phụ thuộc vào α
b) Q= -cos4α(2cos2α -1 -2) +sin4α(1 -2sin2α+2)
= -cos4α(cos2α -2) +sin4α(cos2α +2)
=-cos4α.cos2α +2cos4α +sin4α.cos2α +2sin4α
=cos2α(sin4α -cos4α) +2(sin4α +cos4α)
=cos2α [\(\left(\frac{1-cos^22\text{α}}{2}\right)^2-\left(\frac{1+cos^22\text{α}}{2}\right)^2\)]+2.[\(\left(\frac{1-cos^22\text{α}}{2}\right)^2+ \left(\frac{1+cos^22\text{α}}{2}\right)^2\)]
= -cos2α.cos2α +1+cos22α
= -cos22α +1+cos22α
=1
Vậy Q không phụ thuộc vào α
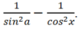
Chọn C.
Ta có: cota + tana) 2 = cot2a + 2.cota.tana + tan2a
= (cot2a + 1) + (tan2a + 1)