Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: a + b + c = 36
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
a/3 = b/4 = c/5 = (a + b + c)/(3 + 4 + 5) = 36/12 = 3
Độ dài ba cạnh của tam giác vuông là:
a/3 = 3 => a = 9
b/4 = 3 => b = 12
c/5 = 3 => c = 15
Diện tích tam giác vuông đó là: 1/2 . a.b = 1/2 . 9. 12 = 54 (đvdt)
Gọi 3 cạnh của tam giác là a ; b ; c thỏa mãn \(\begin{cases}\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\\a+b+c=36\end{cases}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
\(\Rightarrow\begin{cases}a=9\\b=12\\c=15\end{cases}\)
Ta biết trong tam giác vuông , cạnh huyền là cạnh lớn nhất
=> 2 cạnh góc vuông là 9 và 12
\(\Rightarrow S=\frac{9.12}{2}=54\) ( đơn vị diện tích )
Biết các cạnh của hình tam giác tỉ lệ với 4 ; 5 ; 3 và chu vi của nó bằng 120. Tính các cạnh của nó.
gọi các cạnh của tam giác lần lượt là a,b,c .
Theo bài ra : a + b + c = 64 và a,b,c tỉ lệ thuận với 3,6,7
\(\Rightarrow\frac{a}{3}=\frac{b}{6}=\frac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có :
\(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}=\frac{a+b+c}{3+6+7}=\frac{64}{16}=4\)
\(\Rightarrow a=12;b=24;c=28\)
Vậy ...
Gọi a, b, c lần lượt là các cạnh của tam giác đó. Mà a, b, c tỉ lệ thuận với 3, 6, 7 => \(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}\)
Mà chu vi của tam giác đó là 64 cm => a+b+c = 64
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}=\frac{a+b+c}{3+6+7}=\frac{64}{16}=4\)
\(\frac{a}{3}\)=4 => a = 3.4=12
\(\frac{b}{6}\)= 4 => b = 6.4 = 24
\(\frac{c}{7}\)= 4 => c = 7.4 = 28
Vậy a = 12 , b=24 , c = 28
1)\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{b}+1=\frac{c}{d}+1\Leftrightarrow\frac{a+b}{b}=\frac{c+d}{d}\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow ac-ad=ac-bc\Leftrightarrow a\left(c-d\right)=c\left(a-b\right)\Rightarrow\frac{a}{a-b}=\frac{c}{c-d}\)
2) Gọi độ dài các cạnh của tam giác đó là a,b,c thì a : b : c = 3 : 4 : 5 ; a + b + c = 36
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\Rightarrow\hept{\begin{cases}a=3.3=9\\b=3.4=12\\c=3.5=15\end{cases}}\).Vậy tam giác đó có 3 cạnh là 9 cm ; 12 cm ; 15 cm
3)\(\hept{\begin{cases}a:b:c:d=3:4:5:6\\a+b+c+d=3,6\end{cases}\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{d}{6}=\frac{a+b+c+d}{3+4+5+6}=\frac{3,6}{18}=0,2}\)
=> a = 0,2.3 = 0,6 ; b = 0,2.4 = 0,8 ; c = 0,2.5 = 1 ; d = 0,2.6 = 1,2
4)\(\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{3}:5=\frac{y}{2}:5\Leftrightarrow\frac{x}{15}=\frac{y}{10}\)
\(\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{y}{5}:2=\frac{z}{7}:2\Leftrightarrow\frac{y}{10}=\frac{z}{14}\)
\(\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{14}=\frac{x+y+z}{15+10+14}=\frac{184}{39}=4\frac{28}{39}\Rightarrow\hept{\begin{cases}x=4\frac{28}{39}.15=70\frac{10}{13}\\y=4\frac{28}{39}.10=47\frac{7}{39}\\z=4\frac{28}{39}.14=66\frac{2}{39}\end{cases}}\)
Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{kb+b}{kb-b}=\frac{b\left(k+1\right)}{b\left(k-1\right)}=\frac{k+1}{k-1}\left(1\right)\)
\(\frac{c+d}{c-d}=\frac{kd+d}{kd-d}=\frac{d\left(k+1\right)}{d\left(k-1\right)}=\frac{k+1}{k-1}\left(2\right)\)
Từ (1) và (2) => \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
Bài 5:
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
Vậy a = b = c
Gọi ba cạnh của tam giác đó lần lượt là a, b, c (cm)
Ta có: a, b, c tỉ lệ với 2, 3, 4 => a/2 = b/3 = c/4
Vì chu vi tam giác là 81cm =>a+b+c = 81
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/2 = b/3 = c/4 = (a+b+c)/(2+3+4) = 81/9 = 9
=> a = 9x2 = 18; b = 9x3 = 27; c = 9x4 = 36
Vậy ba cạnh của tam giác có số đo lần lượt là 18cm, 27cm và 36cm
Gọi độ dài 3 cạnh tam giác lần lượt là a;b;;c (a;b;c > 0)
Theo bài ra ta có : a + b +c = 81
Lại có \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{81}{9}=9\)
=> a = 2.9 = 18;
b = 3.9 = 27 ;
c = 4.9 = 36
Vậy độ dài 3 cạnh tam giác là 18 cm ; 27 cm ; 36 cm
Bài 1 :
a ) Vì tam giác ABC có chu vi bằng 24
=> AB + AC + BC = 24
hay a + b + c = 24
Vì 3 cạnh của tam giác ABC tỉ lệ với 3,4,5
=> a/3 = b/4 = c/5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
a/3 = b/4 = c/5 = ( a + b + c ) / ( 3 + 4 + 5 ) = 24/12 = 2
=> a = 6 ; b = 8 ; c = 10
b ) Vì a = 6 => a2 = 36
b = 8 => b2 = 64
c = 10 => c2 = 100
MÀ 100 = 36 + 64 hay c2 = a2 + b2
Xét tam giác ABC có c2 = a2 + b2 ( cmt )
=> tam giác ABC là tam giác vuông ( định lí đảo định lí pytago )
Vậy ...
Bài 2 :
Đặt a/b = c/d = t ( t khác 0 ) => a = bt ; c = dt
Khi đó :
\(\frac{5a+5b}{5b}=\frac{5bt+5b}{5b}=\frac{5b\left(t+1\right)}{5b}=t+1\)( 1 )
\(\frac{c^2+cd}{cd}=\frac{\left(dt\right)^2+dtd}{dtd}=\frac{d^2t^2+d^2t}{d^2t}=t+1\)( 2 )
Từ ( 1 ) và ( 2 ) ta có dpcm
b ) ( chứng minh tương tự )
A C B H
Áp dụng định lý Pytago ta có:
\(AC^2=AH^2+HC^2=12^2+16^2=400\)
\(\Rightarrow AC=20\left(cm\right)\)
Và \(BH^2=AB^2-AH^2=13^2-12^2=25\)
\(\Rightarrow BH=5\left(cm\right)\Rightarrow BC=BH+HC=5+16=21\left(cm\right)\)
Vậy \(\hept{\begin{cases}AC=20\left(cm\right)\\BC=21\left(cm\right)\end{cases}}\)
Giải:
Hình bạn tự vẽ nhé.
Xét tam giác ACH vuông tại H có:
AH2 + CH2 = AC2 (định lí Pytago)
AC2 = 122 + 162 = 400
=> AC = \(\sqrt{400}\) = 20 (cm) (vì AC > 0)
Xét tam giác ABH vuông tại H có:
AB2 = AH2 + BH2 (định lí Pytago)
132 = 122 + BH2
=> BH2 = 132 - 122 = 25
=> BH = \(\sqrt{25}\) = 5 (cm)
Ta có: BC = BH + CH
= 5 + 16 = 21 (cm)
=> CABC = AB + BC + AC = 21 + 13 + 20 = 54 (cm)
Vậy CABC = 54cm.
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z
Theo đề bài ta có: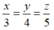
và x + y + z = 36
Theo tính chất của dãy tỉ số bằng nhau ta có:
Chọn đáp án A
Chọn ý A nha!