Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 7: Đổi 30 phút=\(\frac{1}{2}h\)
Gọi quãng đường cần đi là S ( tính theo km, và S>0 )
Khi đó thời gian dự định cần đi là:
\(\frac{S}{30}\)(h)
Thời gian đi nửa quãng đường trước là:
\(\frac{S}{2}\): 30 =\(\frac{S}{60}\)(h)
Thời gian đi nửa quãng đường sau là:
\(\frac{S}{2}:40=\frac{S}{80}\)(h)
Do thời gian giảm đi 30 phút nên:
\(\frac{S}{60}+\frac{S}{80}+\frac{1}{2}=\frac{S}{30}\)
<=> \(\frac{S}{240}=\frac{1}{2}\)
<=> S= 120 (km)
Vậy quãng đường cần tìm là 120 km

\(\dfrac{A}{B}=\dfrac{3x^4+3x^2+x^3+x-3x^2-3+5x-2}{x^2+1}=3x^2+x-3+\dfrac{5x-2}{x^2+1}\)
Để A chia hết cho B thì \(\left(5x-2\right)\left(5x+2\right)⋮x^2+1\)
\(\Leftrightarrow25x^2-4⋮x^2+1\)
\(\Leftrightarrow25x^2+25-29⋮x^2+1\)
\(\Leftrightarrow x^2+1\in\left\{1;29\right\}\)
hay \(x\in\left\{0;2\sqrt{7};-2\sqrt{7}\right\}\)

Bài 3:
a) ta có: \(A=x^2+4x+9\)
\(=x^2+4x+4+5=\left(x+2\right)^2+5\)
Ta có: \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi
\(\left(x+2\right)^2=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy: GTNN của đa thức \(A=x^2+4x+9\) là 5 khi x=-2
b) Ta có: \(B=2x^2-20x+53\)
\(=2\left(x^2-10x+\frac{53}{2}\right)\)
\(=2\left(x^2-10x+25+\frac{3}{2}\right)\)
\(=2\left[\left(x-5\right)^2+\frac{3}{2}\right]\)
\(=2\left(x-5\right)^2+2\cdot\frac{3}{2}\)
\(=2\left(x-5\right)^2+3\)
Ta có: \(\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi
\(2\left(x-5\right)^2=0\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x-5=0\Leftrightarrow x=5\)
Vậy: GTNN của đa thức \(B=2x^2-20x+53\) là 3 khi x=5
c) Ta có : \(M=1+6x-x^2\)
\(=-x^2+6x+1\)
\(=-\left(x^2-6x-1\right)\)
\(=-\left(x^2-6x+9-10\right)\)
\(=-\left[\left(x-3\right)^2-10\right]\)
\(=-\left(x-3\right)^2+10\)
Ta có: \(\left(x-3\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-3\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-3\right)^2+10\le10\forall x\)
Dấu '=' xảy ra khi
\(-\left(x-3\right)^2=0\Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy: GTLN của đa thức \(M=1+6x-x^2\) là 10 khi x=3
Bài 2:
a) \(\left(x+y\right)^2+\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2+\left(x-y\right).\left(x+y\right)\)
\(=\left(x+y\right).\left(x+y+x-y\right)\)
\(=\left(x+y\right).2x\)
c) \(x^2-2xy+y^2-z^2+2zt-t^2\)
\(=\left(x^2-2xy+y^2\right)-\left(z^2-2zt+t^2\right)\)
\(=\left(x-y\right)^2-\left(z-t\right)^2\)
\(=\left[x-y-\left(z-t\right)\right].\left(x-y+z-t\right)\)
\(=\left(x-y-z+t\right).\left(x-y+z-t\right)\)
Chúc bạn học tốt!

3.
- Gọi x(km) là quãng đường AB ( x > 0 )
- Thời gian đi:\(\dfrac{x}{60}\) (h)
- Thời gia về:\(\dfrac{x}{50}\) (h)
Ta có phương trình
\(\dfrac{x}{50}\) - \(\dfrac{x}{60}\) = \(\dfrac{4}{5}\)
\(\Leftrightarrow\) 6x - 5x = 240
\(\Leftrightarrow\) x = 240 (TM)
Vậy quãng đường AB là 240km

B1:a)(3x-5)2-(3x+1)2=8
[(3x-5)+(3x+1)].[(3x-5)-(3x+1)]=8
(3x-5+3x+1)(3x-5-3x-1)=8
9x2-15x-9x2-3x-15x+25+15x+5+9x2-15x-9x2-3x+3x-5-3x-1=8
-36x+24=8
-36x=8-24=16
x=16:(-36)=\(\dfrac{-4}{9}\)
Bài 5:
a: \(=\left(xy-u^2v^3\right)\left(xy+u^2v^3\right)\)
b: \(=\left(2xy^2-3xy^2+1\right)\left(2xy^2+3xy^2-1\right)\)
\(=\left(1-xy^2\right)\left(5xy^2-1\right)\)
Bài 6:
a: \(\left(a+b+c-d\right)\left(a+b-c+d\right)\)
\(=\left(a+b\right)^2+\left(c-d\right)^2\)
\(=a^2+2ab+b^2+c^2-2cd+d^2\)
b: \(\left(a+b-c-d\right)\left(a-b+c-d\right)\)
\(=\left(a-d\right)^2-\left(b-c\right)^2\)
\(=a^2-2ad+d^2-b^2+2bc-c^2\)

A B E C F
a) Xét \(\Delta\)EBA và \(\Delta\)ABC có:
\(\widehat{BEA}=\widehat{BAC}\left(=90^o\right)\)
\(\widehat{B}\) là góc chung
\(\Rightarrow\) \(\Delta\)EBA đòng dạng vs \(\Delta\)ABC (g - g)
\(\Rightarrow\) \(\dfrac{BE}{AB}=\dfrac{AB}{BC}\)
\(\Rightarrow\) AB2 = BE . BC
b) Trong \(\Delta\)ABC vuông tại A có:
BC2 = AB2 + AC2
= 32 . 42
= 25
\(\Rightarrow\) BC = \(\sqrt{25}\) = 5(cm)
Vì: AB2 = BC.BE (cmt)
\(\Rightarrow\) BE = \(\dfrac{AB^2}{BC}\)
= \(\dfrac{3^2}{5}\) = 1.8(cm)
Xét \(\Delta\)BEA vuông tại E có:
AE2 = AB2 + BE2
= 32 + 1.82
= \(\dfrac{306}{25}\)
\(\Rightarrow\)AE = \(\sqrt{\dfrac{306}{25}}\) = \(\dfrac{3\sqrt{34}}{5}\)(cm)
c) Trong \(\Delta\)ABC có BF là tia phân giác của góc B
\(\Rightarrow\) \(\dfrac{AF}{AB}=\dfrac{CF}{BC}\)
Áp dụng t/chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{AF}{AB}=\dfrac{CF}{BC}\)\(=\dfrac{AF+CF}{AB+BC}=\dfrac{AC}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AF}{3}=\dfrac{1}{2}\Rightarrow AF=1.5\left(cm\right)\)
Trong \(\Delta\)ABF vuông tại A có:
BF2 = AB2 + AF2
= 32 + 1.52
= 11.25
\(\Rightarrow\) BF = \(\sqrt{11.25}\) = \(\dfrac{3\sqrt{5}}{2}\)(cm)
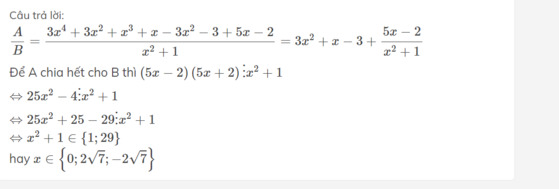
Bài 1 Gọi thời gian đi từ A đến B lúc đi là x (x>0)(giờ)
Theo bài ta có : \(35x=\left(35+5\right)\left(x-\dfrac{1}{4}\right)\)
=> \(35x=40x-10\)
=> \(5x=10\Rightarrow x=2\) (giờ) (TM)
Quãng đường AB dài là : s=35.2=70km
Bài 2
Khi xe hơi bắt đầu đuổi theo thì xe máy đã đi được: \(30.\dfrac{2}{3}=20\left(km\right)\)
Mỗi giờ xe hơi đi hơn xe máy số km là: 45-30 = 15 (km)
Xe hơi đuổi kịp xe máy sau: 20 : 15 = \(\dfrac{4}{3}\left(h\right)=1h20'\)