Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Giả sử ba số hạng a, b, c lập thành cấp số cộng thỏa yêu cầu, khi đó b, a, c theo thứ tự đó lập thành cấp số nhân công bội q. Ta có
a + c = 2 b a = b q ; c = b q 2 ⇒ b q + b q 2 = 2 b ⇔ b = 0 q 2 + q − 2 = 0 .
Nếu b = 0 ⇒ a = b = c = 0 nên a, b, c là cấp số cộng công sai d= 0 (vô lí).
Nếu q 2 + q − 2 = 0 ⇔ q = 1 hoặc q= -2. Nếu q = 1 ⇒ a = b = c (vô lí), do đó q = -2.

Ta có hệ phương trình:
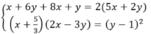
Từ đó ta suy ra
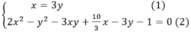
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B

Ba số x, y, z lập thành một cấp số nhân nên:
y = x.q và z = y.q = x.q2 ( q là công bội)
Ba số x, 2y, 3z lậo thành một cấp số cộng nên:
x + 3z = 4y ⇔ x + 3.(xq2) = 4.(x.q)
⇔ x. (1 + 3q2 – 4q) = 0 ⇔ x = 0 hay 3q2 – 4q + 1 = 0
Nếu x = 0 thì x = y= z= 0, q là một số tùy ý
Nếu x ≠ 0 thì 3q2– 4q + 1 = 0 ⇔\(\Leftrightarrow\left[{}\begin{matrix}q=1\\q=\dfrac{1}{3}\end{matrix}\right.\).
Công bội của cấp số nhân là \(q=1\) hoặc \(q=\dfrac{1}{3}\).

Chọn A
+ Ba số x + 6 y ,5 x + 2 y ,8 x + y lập thành cấp số cộng nên
x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + 7 y = 10 x + 4 y ⇔ x = 3 y
+ Ba số x + 5 3 , y − 1,2 x − 3 y lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .
Thay x= 3y vào ta được :
3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y = y 2 − 2 y + 1 ⇔ 9 y 2 + 5 y − y 2 + 2 y − 1 = 0
⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc y = 1 8 .
Với y= -1 thì x= - 3; với y = 1 8 thì x = 3 8 .

Lời giải:
Ta có:
$y=xq$
$z=yq=xq^2$
Và:
$2y=x+d$
$3z=2y+d=x+2d$
$\Rightarrow 2xq=x+d$ và $3xq^2=x+2d$
$\Rightarrow 3xq^2-2xq=d$
$\Leftrightarrow xq(3q-2)=d$
Khi đó, thay vô $2xq=x+d$ thì:
$\frac{2d}{3q-2}=\frac{d}{q(3q-2)}+d$
$\Leftrightarrow \frac{2}{3q-2}=\frac{1}{q(3q-2)}+1$ (do $d\neq 0$)
$\Leftrightarrow 2q=1+q(3q-2)$
$\Leftrightarrow 3q^2-4q+1=0$
$\Leftrightarrow (q-1)(3q-1)=0$
Vì $q\neq 1$ nên $q=\frac{1}{3}$

Theo giả thiết : \(\begin{cases}xy=3^2\\x^4=y\sqrt{3}\end{cases}\) \(\Leftrightarrow\begin{cases}y=\frac{9}{x}\\x^4=\frac{9\sqrt{3}}{x}\end{cases}\) \(\Leftrightarrow\begin{cases}y=\frac{9}{x}\\x^5=9\sqrt{3}\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\sqrt[5]{\sqrt{3^5}}\\y=\frac{3^2}{x}\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\sqrt{3}\\y=3\sqrt{3}\end{cases}\)
Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .