Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách

Đáp án A
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố“3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là
![]()
Vậy xác suất cần tìm là
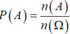
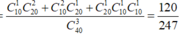

Chọn B
Số phần tử của không gian mẫu là ![]()
- Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”
- Số phần tử của biến cố A là
![]()
Vậy xác suất để xảy ra biến cố A là
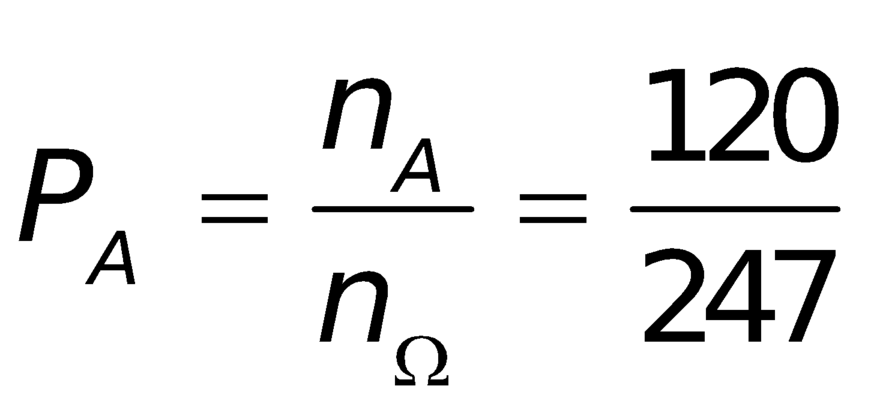 .
.

\(\frac{P_nC_n^k}{n!A_n^k}=\frac{n!.\frac{n!}{k!\left(n-k\right)!}}{n!.\frac{n!}{\left(n-k\right)!}}=\frac{1}{k!}\)
Chắc là bạn ghi nhầm đề

Phép thử T được xét là: "Hai xạ thủ cùng bắn vào bia".
Theo đề ra ta có = "Người thứ k không bắn trúng", k = 1, 2. Từ đó ta có:
a) A = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai không bắn trúng". Suy ra A = .
.
Tương tự, ta có B = "Cả hai đều bắn trúng" = .
.
Xét C = "Có đúng một người bắn trúng", ta có C là hợp của hai biến cố sau:
"Người thứ nhất bắn trúng và người thứ hai bắn trượt" = A1 . .
"Người thứ nhất bắn trượt và người thứ hai bắn trúng" = . A2 .
Suy ra C = A1 . ∪
. A2 .
Tương tự, ta có D = A1 ∪ A2 .
b) Gọi là biến cố: " Cả hai người đều bắn trượt". Ta có
=
.
= A.
Hiển nhiên B ∩ C = Φ nên suy ra B và C xung khắc với nhau.
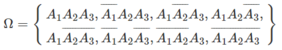
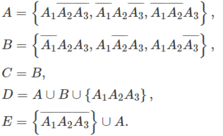

- Mỗi kết quả phải mô tả mỗi học sinh đạt hay không đạt. Các khả năng có thể xảy ra là: cả ba học sinh đều đạt, hoặc chỉ có hai học sinh đạt, hoặc chỉ có một học sinh đạt, hoặc không có học sinh nào đạt.
Ω = A 1 A 2 A 3 , A 1 ¯ A 2 A 3 , A 1 A 2 ¯ A 3 , A 1 A 2 A 3 ¯ , A 1 A 2 A 3 ¯ , A 1 ¯ A 2 A 3 ¯ , A 1 A 2 ¯ A 3 , A 1 A 2 A 3 ¯
Nhận xét: học sinh có thể nhầm lẫn:
- Chỉ mô tả kết quả của 1 học sinh (phương án A)
- Hoặc mô tả kết quả của hai học sinh (phương án D)
- Hoặc mô tả kết quả của ba học sinh nhưng chưa đầy đủ (phương án B)
Chọn C