Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Yêu cầu bài toán tương đương với
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}+\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}+\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=0\) (1)
Gọi \(X_1\) là điểm trên đường thẳng AB sao cho \(XX_1\) // \(\Delta\) (tức là \(X_1\) là hình chiếu song song của điểm X trên đường thẳng AB theo phương chiếu \(\Delta\) .
Khi đó \(A_1\equiv A,B_1\equiv B,A'_1\equiv B'_1\equiv C'_1,\)
Theo định lí Ta-lét ta có :
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}=\frac{\overrightarrow{G_1A}}{\overrightarrow{G_1A_1'}};\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}=\frac{\overrightarrow{G_1B}}{\overrightarrow{G_1B_1'}};\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=\frac{\overrightarrow{G_1C_1}}{\overrightarrow{G_1C_1'}};\)
Suy ra
\(\frac{\overrightarrow{GA}}{\overrightarrow{GA'}}+\frac{\overrightarrow{GB}}{\overrightarrow{GB'}}+\frac{\overrightarrow{GC}}{\overrightarrow{GC'}}=\frac{\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}}{\overrightarrow{G_1A'_1}}=0\)(2)
Lại do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) nên \(\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}=0\)
Vậy \(\overrightarrow{G_1A}+\overrightarrow{G_1B}+\overrightarrow{G_1C_1}=0\)
Từ (1) và (2) suy ra được điều cần chứng minh

25.
H là hình chiếu của S lên (ABC)
Do \(SA=SB=SC\Rightarrow HA=HB=HC\)
\(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
26.
\(\left\{{}\begin{matrix}AB\perp BC\\AB\perp CD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\) \(\Rightarrow AB\perp BD\)
\(\Rightarrow\Delta ABD\) vuông tại B
Pitago tam giác vuông BCD (vuông tại C):
\(BC^2+CD^2=BD^2\Rightarrow BD^2=b^2+c^2\)
Pitago tam giác vuông ABD:
\(AD^2=AB^2+BC^2=a^2+b^2+c^2\)
\(\Rightarrow AD=\sqrt{a^2+b^2+c^2}\)
23.
Gọi H là chân đường cao hạ từ S xuống BC
\(\Rightarrow BH=SB.cos30^0=3a\) ; \(SH=SB.sin30^0=a\sqrt{3}\) ; \(CH=4a-3a=a\)
\(\Rightarrow BC=4HC\Rightarrow d\left(B;\left(SAC\right)\right)=4d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HE\perp AC\) ; từ H kẻ \(HF\perp SE\Rightarrow HF\perp\left(SAC\right)\)
\(\Rightarrow HF=d\left(H;\left(SAC\right)\right)\)
\(HE=CH.sinC=\frac{CH.AB}{AC}=\frac{a.3a}{5a}=\frac{3a}{5}\)
\(\frac{1}{HF^2}=\frac{1}{HE^2}+\frac{1}{SH^2}\Rightarrow HF=\frac{HE.SH}{\sqrt{HE^2+SH^2}}=\frac{3a\sqrt{7}}{14}\)
\(\Rightarrow d\left(B;\left(SAC\right)\right)=4HF=\frac{6a\sqrt{7}}{7}\)
24.
\(SA=SC\Rightarrow SO\perp AC\)
\(SB=SD\Rightarrow SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)

Đáp án A
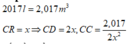
Số tiền để xây đáy là: ![]()
Số tiền để xây thân bể là: 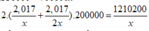
Số tiền để xây nắp bể là : ![]()
Số tiền để xây bể là :
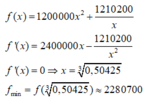
Đáp án D
Gọi kích thước của đáy là a;b(a < b).Khi đó chiều cao của hố là h = 2a. Ta có: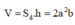
Diện tích nguyên vật liệu cần dùng là:
Xét hàm số:
Xét hàm số:
Bảng biến thiên:
0 10
+ ∞
- 0 +
Vậy khi a = 10 thì hố ga được xây sẽ tiết kiệm nguyên liệu nhất.