Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a, Ta có:
\(\dfrac{x.\dfrac{xy}{x-y}}{x+\dfrac{xy}{x-y}}-\dfrac{y.\dfrac{xy}{x-y}}{y-\dfrac{xy}{x-y}}\)
\(=\dfrac{\dfrac{x^2y}{x-y}}{x+\dfrac{xy}{x-y}}-\dfrac{\dfrac{xy^2}{x-y}}{y-\dfrac{xy}{x-y}}\)
\(=\dfrac{\left(\dfrac{x^2y}{x-y}\right)\left(y-\dfrac{xy}{x-y}\right)-\left(\dfrac{xy^2}{x-y}\right)\left(x+\dfrac{xy}{x-y}\right)}{\left(x+\dfrac{xy}{x-y}\right)\left(y-\dfrac{xy}{x-y}\right)}\)
\(=\dfrac{\dfrac{x^2y^2}{x-y}-\dfrac{x^3y^2}{\left(x-y\right)^2}-\dfrac{x^2y^2}{x-y}-\dfrac{x^2y^3}{\left(x-y\right)^2}}{xy-\dfrac{x^2y}{x-y}+\dfrac{xy^2}{x-y}-\dfrac{x^2y^2}{\left(x-y\right)^2}}\)
\(=\dfrac{-\left(\dfrac{x^3y^2+x^2y^3}{\left(x-y\right)^2}\right)}{xy-\left(\dfrac{x^2y-xy^2}{x-y}\right)-\dfrac{x^2y^2}{\left(x-y\right)^2}}\)
\(=-\dfrac{\dfrac{x^2y^2\left(x+y\right)}{\left(x-y\right)^2}}{xy-\left(\dfrac{xy\left(x-y\right)}{\left(x-y\right)}\right)-\dfrac{x^2y^2}{\left(x-y\right)^2}}\)
\(=\dfrac{\dfrac{x^2y^2\left(x+y\right)}{\left(x-y\right)^2}}{\dfrac{x^2y^2}{\left(x-y\right)^2}}=x+y\)
Chúc bạn học tốt!! Làm một câu mà toát cả mồ hôi!

a, Ta có : \(A=\frac{1}{x+2}-\frac{2x}{4-x^2}+\frac{3}{x-2}\)
\(=\frac{1}{x+2}-\frac{2x}{\left(2-x\right)\left(x+2\right)}+\frac{3}{x-2}\)
\(=\frac{x-2}{\left(x+2\right)\left(x-2\right)}+\frac{2x}{\left(x-2\right)\left(x+2\right)}+\frac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x-2+2x+3x+6}{\left(x-2\right)\left(x+2\right)}=\frac{6x+4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra : \(M=\frac{6x+4}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{3x+2}\)
\(=\frac{2\left(3x+2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)\left(3x+2\right)}=\frac{2}{x-2}\)

Để \(Q\) nhỏ nhất => \(m;n\) nhỏ nhất
=>\(m^2+n^2\) nhỏ nhất
Mà \(m^2;n^2\ge0\)
Suy ra để \(Q\) nhỏ nhất thì

a) \(A=\dfrac{mn^2+n^2\left(n^2-m\right)+1}{m^2n^4+2n^4+m^2+2}\)
\(A=\dfrac{mn^2+n^4-mn^2+1}{n^4\left(m^2+2\right)+m^2+2}=\dfrac{n^4+1}{\left(m^2+2\right)\left(n^4+1\right)}=\dfrac{1}{m^2+2}\)
b) CM \(\dfrac{1}{m^2+2}>0\)
ta có \(\left\{{}\begin{matrix}m^2+2>0\\1>0\end{matrix}\right.\forall m\in R\)
\(\Rightarrow\dfrac{1}{m^2+2}>0\forall m\in R\)
vậy đpcm
c) \(A=\dfrac{1}{m^2+2}=\dfrac{2}{2m^2+4}=\dfrac{m^2+2-m^2}{2m^2+4}=\dfrac{1}{2}-\dfrac{m^2}{2m^2+4}\le\dfrac{1}{2}\forall m\in R\)
dấu '=' xảy ra khi m=0
vậy \(A_{max}=\dfrac{1}{2}\) khi m=0

a: Khi x=1 thì \(A=\dfrac{1+1}{2}=1\)
b: Để A=2 thì x+1=4
=>x=3
c: \(B=\dfrac{2+x-2+x}{x\left(x-2\right)}=\dfrac{2x}{x\left(x-2\right)}=\dfrac{2}{x-2}\)
d: C=A*B=2/(x-2)*x+1/2=x+1/x-2
Để C la số nguyên thì x-2+3 chia hết cho x-2
=>\(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;5;-1;1\right\}\)

a, \(I=s\left(s^2-t\right)+\left(t^2+s\right)=s^3-st+t^2+s\)
Thay t = -1 và s = 1 vào biểu thức trên ta được :
\(1+1+1+1=4\)
b, \(N=u^2\left(u-v\right)-v\left(v^2-u^2\right)=u^2\left(u-v\right)+v\left(u+v\right)\left(u-v\right)\)
\(=\left(u-v\right)\left(u^2+v\left(u+v\right)\right)\)
Thay \(u=0,5=\frac{1}{2};v=-\frac{1}{2}\)
\(=\left(\frac{1}{2}+\frac{1}{2}\right).\frac{1}{4}=\frac{1}{4}\)

Bài 1:
a) x≠2x≠2
Bài 2:
a) x≠0;x≠5x≠0;x≠5
b) x2−10x+25x2−5x=(x−5)2x(x−5)=x−5xx2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
c) Để phân thức có giá trị nguyên thì x−5xx−5x phải có giá trị nguyên.
=> x=−5x=−5
Bài 3:
a) (x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)(x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)
=(x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5=(x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5
=(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5=(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5
=(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5=(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5
=[(x+1)2+6−(x2+2x−3)]⋅25=[(x+1)2+6−(x2+2x−3)]⋅25
=[(x+1)2+6−x2−2x+3]⋅25=[(x+1)2+6−x2−2x+3]⋅25
=[(x+1)2+9−x2−2x]⋅25=[(x+1)2+9−x2−2x]⋅25
=2(x+1)25+185−25x2−45x=2(x+1)25+185−25x2−45x
=2(x2+2x+1)5+185−25x2−45x=2(x2+2x+1)5+185−25x2−45x
=2x2+4x+25+185−25x2−45x=2x2+4x+25+185−25x2−45x
=2x2+4x+2+185−25x2−45x=2x2+4x+2+185−25x2−45x
=2x2+4x+205−25x2−45x=2x2+4x+205−25x2−45x
c) tự làm, đkxđ: x≠1;x≠−1
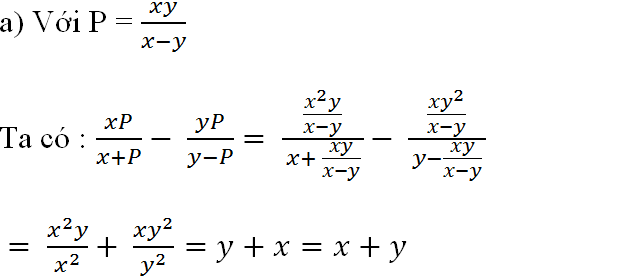
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.