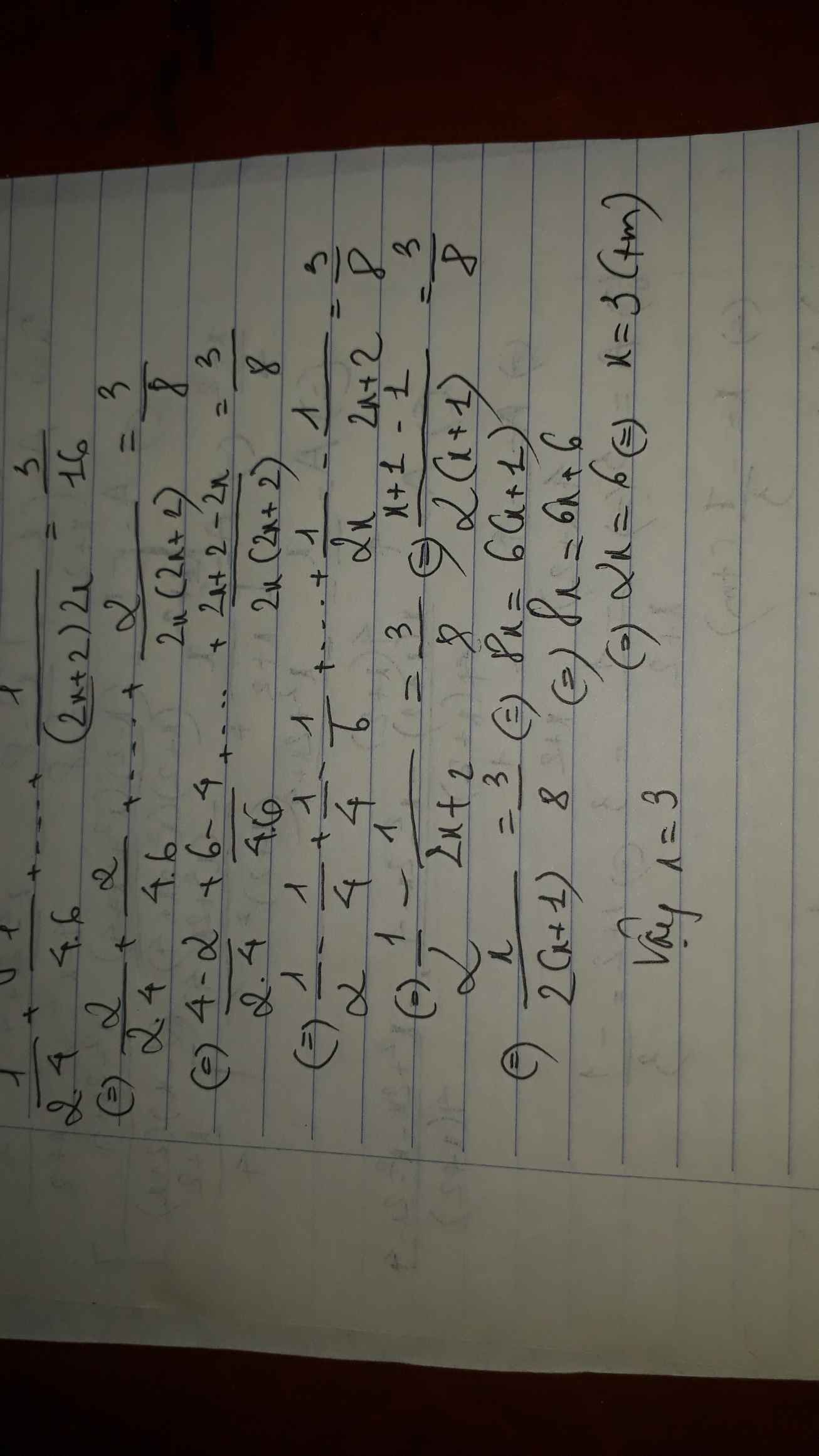TV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MK
1
LB
4 tháng 5 2018
\(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{\left(2x-2\right)2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{4-2}{2.4}+\dfrac{6-4}{4.6}+...+\dfrac{2x-\left(2x-2\right)}{\left(2x-2\right)2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+..+\dfrac{1}{2x-2}-\dfrac{1}{2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{-1}{2x}=\dfrac{-1}{4}\)
\(\Rightarrow x=2\)
S
4 tháng 5 2018
Ta có: \(\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{\left(2x-2\right).2x}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2x-2}-\dfrac{1}{2x}\right)=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2x}\right)=\dfrac{1}{8}\Rightarrow\dfrac{1}{2}.\dfrac{x-1}{2x}=\dfrac{1}{8}\Rightarrow\dfrac{x-1}{4x}=\dfrac{1}{8}\)
\(\Rightarrow8\left(x-1\right)=4x\Rightarrow8x-8=4x\Rightarrow4x=8\Rightarrow x=2\)
LM
26 tháng 9 2016
A = {10 ; 12 ; 14 ; 16 ; 18}
B = {199 ; 201 ; 203 ; 205}
C = {5 ; 6 ; 7 ; 8}
D = {0}
25 tháng 1 2017
Bài 1:
a) Chỗ y6 là 6.y hay là y6
b) \(2\left(x-1\right)-3\left(2x+2\right)-4\left(2x+3\right)=16\)
\(\Rightarrow2x-2-6x-6-8x-12=16\)
\(\Rightarrow\left(2x-6x-8x\right)-\left(2+6+12\right)=16\)
\(\Rightarrow-12x-20=16\)
\(\Rightarrow-12x=36\)
\(\Rightarrow x=-3\)
Vậy x = -3
c) \(\left(x-5\right)^{x+1}-\left(x-5\right)^{x+13}=0\)
\(\Rightarrow\left(x-5\right)^{x+1}\left[1-\left(x-5\right)^{12}\right]=0\)
\(\Rightarrow\left(x-5\right)^{x+1}=0\) hoặc \(1-\left(x-5\right)^{12}=0\)
+) \(\left(x-5\right)^{x+1}=0\Rightarrow x-5=0\Rightarrow x=5\)
+) \(1-\left(x-5\right)^{12}=0\Rightarrow\left(x-5\right)^{12}=1\)
\(\Rightarrow x-5=\pm1\)
+) \(x-5=1\Rightarrow x=6\)
+) \(x-5=-1\Rightarrow x=4\)
Vậy \(x\in\left\{6;4\right\}\)
Bài 2: a, thiếu dữ liệu
b) Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{a+b+c}=1\)
\(\left[\begin{matrix}\frac{a}{b}=1\\\frac{b}{c}=1\\\frac{c}{a}=1\end{matrix}\right.\Rightarrow\left[\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\Rightarrow a=b=c\)
Ta có: \(\frac{a^3b^2c^{1930}}{a^{1935}}=\frac{a^3a^2a^{1930}}{a^{1935}}=\frac{a^{1935}}{a^{1935}}=1\)
Vậy \(\frac{a^3b^2c^{1930}}{a^{1935}}=1\)
NM
3
15 tháng 10 2021
\(S=8+8^3+...+8^{2x+1}\\ \Rightarrow64S=8^3+8^5+...+8^{2x+3}\\ \Rightarrow64S-S=\left(8^3+8^5+...+8^{2x+3}\right)-\left(8+8^3+...+8^{2x+1}\right)\\ \Rightarrow63S=8^{2x+3}-8\\ \Rightarrow S=\dfrac{8^{2x+3}-8}{63}\)
4 tháng 10 2017
a)
(2x-1)4 = 34
=>2x-1 = 3
2x = 3+1
2x = 4
x = 2
b)
(3x-1)3 = 53
=> 3x-1 = 5
3x = 5+1
3x = 6
x = 2
c)
4x-1 . 42 = 45
4x-1 = 45 : 42
4x-1 = 43
=> x-1 = 3
x= 4
d)
3.34 nhỏ hơn hoặc bằng 32x nhỏ hơn hoặc bằng 33 . 35
35 nhỏ hơn hoặc bằng 32x nhỏ hơn hoặc bằng 38
=> 2x = 5 ; 6 ;7; 8
Nếu 2x = 5 thì x = 5:2 (loại)
Nếu 2x = 6 thì x = 3 ( thỏa mãn )
Nếu 2x = 7 thì x = 7: 2 ( loại)
Nếu 2x = 8 thì x = 4 ( thỏa mãn )
=> x= 3:4
4 tháng 10 2017
a) \(\left(2x-1\right)^4=81\)
\(\left(2x-1\right)^4=3^4\)
\(\Rightarrow2x-1=3\)
\(\Rightarrow2x=4\)
\(\Rightarrow x=2\)
vay \(x=2\)
b) \(\left(3x-1\right)^3=125\)
\(\left(3x-1\right)^3=5^3\)
\(\Rightarrow3x-1=5\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
vay \(x=2\)
c) \(4^{x-1}.16=1024\)
\(4^{x-1}=\frac{1024}{16}\)
\(4^{x-1}=64\)
\(4^{x-1}=4^3\)
\(\Rightarrow x-1=3\)
\(\Rightarrow x=4\)
vay \(x=4\)
d) \(3.81\le9^x\le27.243\)
\(3.3^4\le9^x\le3^3.3^5\)
\(3^5\le3^{2x}\le3^8\)
\(\Rightarrow5\le2x\le8\)
\(\Rightarrow\orbr{\begin{cases}2x\le8\\2x\ge5\end{cases}}\Rightarrow\orbr{\begin{cases}x\le4\\x\ge\frac{5}{2}\end{cases}}\Rightarrow\frac{5}{2}\le x\le8\)
vay \(\frac{5}{2}\le x\le8\)