Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt x=B'C(km), 0<=x<=9
=>\(BC=\sqrt{x^2+36};AC=9-x\)
Chi phí xây dựng dường ống là:
\(C\left(x\right)=130000\sqrt{x^2+36}+50000\left(9-x\right)\left(USD\right)\)
Hàm C(x) xác định và liên tục trên [0;9] và \(C'\left(x\right)=10000\left(\dfrac{13x}{\sqrt{x^2+36}}-5\right)\)
C'(x)=0
=>13x=5 căn x^2+36
=>x=5/2

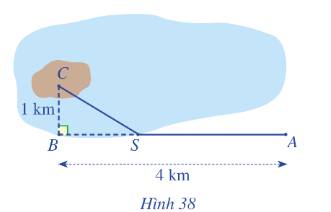
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
\( \Rightarrow BS = 4 - x\)(km)
\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)
Tổng số tiền từ A đến C là:
\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)
Khi đó ta có phương trình:
\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16\)
\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16 - 3x\)
\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)
Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)
=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)} = 1,25\)
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

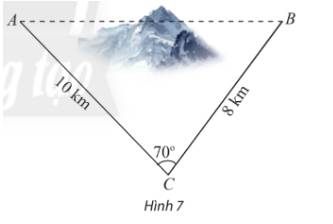
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)

\(\Delta_1\) nhận \(\left(2;1\right)\) là 1 vppt; \(\Delta_2\) nhận \(\left(1;m\right)\) là 1 vtpt
a/ Để 2 đường thẳng song song \(\Rightarrow2m=1\Rightarrow m=\frac{1}{2}\)
Khi đó pt \(\Delta_2\) viết lại: \(2x+y+2=0\)
Khoảng cách 2 đường thẳng: \(d=\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}=\frac{\left|-3-2\right|}{\sqrt{2^2+1^2}}=\sqrt{5}\)
b/Với \(m=2\Rightarrow\Delta_2\) nhận \(\left(1;2\right)\) là 1 vtpt
\(cos\left(\Delta_1;\Delta_2\right)=\frac{\left|2.1+1.2\right|}{\sqrt{2^2+1^2}.\sqrt{1^2+2^2}}=\frac{4}{5}\)
\(\Rightarrow sin\left(\Delta_1;\Delta_2\right)=\sqrt{1-\left(\frac{4}{5}\right)^2}=\frac{3}{5}\)
c/ Chắc là k/c từ gốc O
\(d\left(O;\Delta_1\right)=\frac{\left|2.0+1.0-3\right|}{\sqrt{2^2+1^2}}=\frac{3}{\sqrt{5}}\)
\(d\left(O;\Delta_2\right)=\frac{\left|1.0+m.0+1\right|}{\sqrt{1+m^2}}=\frac{1}{\sqrt{1+m^2}}\)
\(\Rightarrow\frac{1}{\sqrt{1+m^2}}=\frac{6}{\sqrt{5}}\Leftrightarrow1+m^2=\frac{5}{36}\Leftrightarrow m^2=-\frac{29}{36}< 0\)
Không tồn tại m thỏa mãn
d/ I là điểm nào bạn?