Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>AH=DE và AH cắt DE tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và DE
b: ΔHDB vuông tại D có DI là trung tuyến
nên DI=HI=IB
Xét ΔIDO và ΔIHO có
ID=IH
DO=HO
IO chung
=>ΔIHO=ΔIDO
c: góc IDE=góc IDH+góc EDH
=góc IHD+góc EAH
=góc HAC+góc HCA=90 độ
=>ID vuông góc DE
góc KED=góc KEH+góc DEH
=góc KHE+góc DAH
=góc HAB+góc HBA=90 độ
=>KE vuông góc ED
=>ID//KE
=>DIKE là hình thang

a) Cm. AH = DE
Ta có: HD vuông góc với BA (gt)
ED vuông góc với BA ( BA vuông góc với AC; E thuộc AC)
=> HD // EA
Ta lại có: DA vuông góc với AC ( BA vuông góc với AC; D thuộc AB)
HE vuông góc với AC (gt)
=> DA // HE
Xét tứ giác DHEA, có;
* HD // EA (cmt)
* DA // HE (cmt)
=> DHEA là hình bình hành (định nghĩa)
=> DE = AH (tính chất của đường chéo) (đpcm)
b) Gọi O là giao điểm của 2 đường chéo DE, AH của hình bình hành DHEA.
Xét tam giác HEC vuông tại E, có:
* K là trung điểm của HC (gt)
=> EK = KH = KC (trung tuyến của tam giác vuông bằng 1/2 cạnh huyền)
=> DI = IH = IB ( chứng minh tương tự)
Xét tam giác DIO và tam giác HIO, có:
* DI = IH (cmt)
* IO là cạnh chung
* OD = OH (DHEA là hình bình hành)
=> tam giác DIO = tam giác HIO (c.c.c)
=> góc IHO = góc IDO ( yếu tố tương ứng)
Mà góc IHO = 90 độ (AH là đường cao)
=> góc IDO = 90 độ
=> ID vuông góc với DE (1)
Xét tam giác HOK và tam giác EOK, có:
* HO = EO (DHEA là hình bình hành)
* OK là cạnh chung
* KH = KE (cmt)
=> tam giác HOK = tam giác EOK (c.c.c)
=> góc OHK = góc OEK ( yếu tố tương ứng)
Mà góc OHK = 90 độ (AH là đường cao)
=> góc OEK = 90 độ
=> KE vuông góc với DE (2)
Từ (1), (2) => ID // KE (từ vuông góc đến song song) (đpcm).

a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

Xét tứ giác AEHD, có:
∠A = ∠E = ∠D = 90°
=> tứ giác AEHD là hình chữ nhật.
O là giao điểm hai đường chéo hcn AEHD
=> OD = OH (1).
DI là đường trung tuyến ứng với cạnh huyền của Δ vuông DHB
=> DI = 1/2 BH = IH (2).
Xét Δ IDO và Δ IHO, có:
OD = OH (1).
OI là cạnh chung.
DI = IH (2).
=> Δ IDO = Δ IHO (đpcm).
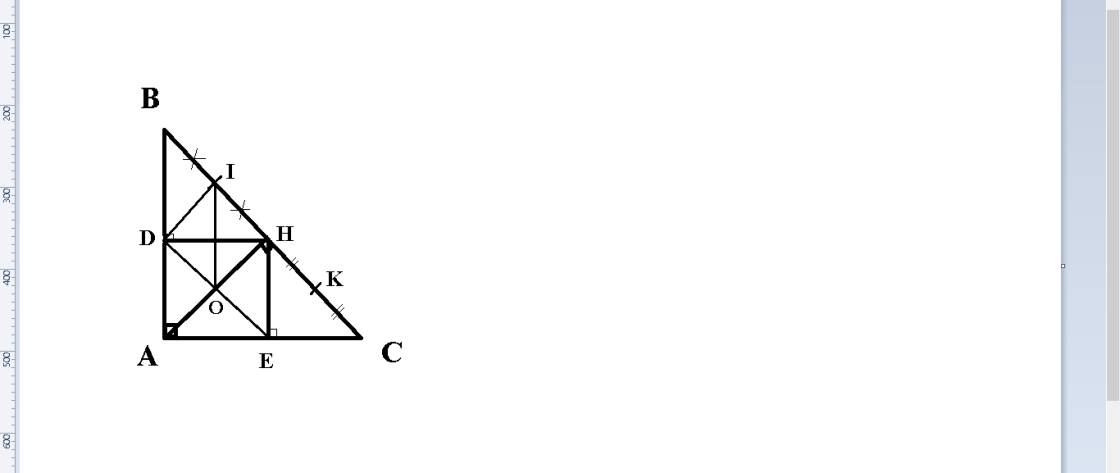
(bồ xem thử ổn hông nhe).

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ΔHDB vuông tại D
mà DI là đường trung tuyến
nên \(DI=IH=IB\)
Xét ΔIHD có IH=ID
nên ΔIHD cân tại I
=>\(\widehat{IHD}=\widehat{IDH}\)
mà \(\widehat{IHD}=\widehat{HCA}\)(hai góc đồng vị, HD//AC)
nên \(\widehat{IDH}=\widehat{HCA}\)
ADHE là hình chữ nhật
=>\(\widehat{EAH}=\widehat{EDH}\)
=>\(\widehat{EDH}=\widehat{HAC}\)
\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)
\(=\widehat{HAC}+\widehat{HCA}\)
\(=90^0\)
=>DI\(\)\(\perp\)DE
c: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên EK=KH=KC
Xét ΔKEH có KE=KH
nên ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{CBA}\)(hai góc đồng vị, HE//AB)
nên \(\widehat{KEH}=\widehat{CBA}=\widehat{HBA}\)
ADHE là hình chữ nhật
=>\(\widehat{HAD}=\widehat{HED}\)
=>\(\widehat{HED}=\widehat{HAB}\)
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{HAB}+\widehat{HBA}=90^0\)
=>KE\(\perp\)DE
Ta có: KE\(\perp\)DE
ID\(\perp\)KE
Do đó: ID//KE
Xét tứ giác KEDI có
KE//DI
KE\(\perp\)ED
Do đó: KEDI là hình thang vuông
d: DI=1cm
mà HB=2DI
nên HB=2*1=2=2cm
EK=4cm
mà CH=2EK
nên \(CH=2\cdot4=8cm\)
BC=BH+CH
=2+8
=10cm
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot6\cdot10=30\left(cm^2\right)\)

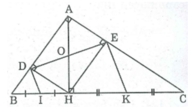
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).

a) chứng minh AH = DE
Xét tứ giác ADHE, ta có
góc HDA = góc DAE = góc AEH = 90o
nên tứ giác ADHE là hình chữ nhật
AH và DE là hai đường chéo trong hình chữ nhật ADHE nên chúng bằng nhau
b) chứng minh DIKE là hình thang vuông
* Gọi F là giao điểm của AH và DE
theo tính chất của đường chéo trong hình chữ nhật thì F là trung điểm của AH và DE, do đó tam giác FDH là tam giác cân tại F
nên góc FHD = góc FDH (1)
* DI là trung tuyến trong tam giác DBH vuông tại D nên DI = IH, do đó tam giác IDH là tam giác cân tại I
nên góc IHD = góc IDH (2)
* mặt khác góc IHD + góc FHD = góc FHI = 90o (3)
từ (1), (2), (3) suy ra góc IDH + góc FDH = góc IDF = 90o
chứng minh tương tự ta được góc FEK = 90o
tứ giác DIKE có 2 góc kề nhau là góc IDF và góc FEK đều là góc vuông nên nó là hình thang vuông.
c) tính độ dài đường trung bình của hình thang DIKE (tạm gọi là y)
y = 0.5 (ID + KE) = 0.5 (0.5 BH + 0.5 CH) = 0.25 BC
theo định lý pytago thì BC2 = AB2 + AC2 = 100 => BC = 10 => y = 2.5.
Cho mk hỏi tại sao DI là trung tuyến của tam giác vuông DBH thì tại sao mà DI lại = IH đc ?