Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phân tích: Ta nhận thấy: Nửa chu vi = Chiều dài + Chiều rộng
Dạng toán: Tìm hai số khi biết Tổng và tỉ số của 2 số đó
( Tổng = 64, Tỉ số giữa Chiều rộng và Chiều dài là 3/5, trong đó chiều rộng tương ứng với 3 phần, chiều dài tương ứng với 5 phần)
Giải: Theo bài ra ta có sơ đồ: ( vẽ theo hướng dẫn)
Tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Giá trị của 1 phần là:
64 : 8 = 8 (m)
Chiều rộng mảnh đất hình chữ nhật là:
8 x 3 = 24 (m)
Chiều dài mảnh đất hình chữ nhật là:
64 – 24 = 40 (m)
Diện tích mảnh đất hình chữ nhật là:
60 x 24 = 1440 (m2)
Đáp số: 1440 m2

Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của hình chữ nhật(Điều kiện: a>0; b>0)
Vì chiều dài bằng \(\dfrac{5}{3}\) chiều rộng nên ta có phương trình: \(a=\dfrac{5}{3}b\)(1)
Vì diện tích là 240m2 nên ta có phương trình: ab=240(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a=\dfrac{5}{3}b\\ab=240\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}b\\\dfrac{5}{3}\cdot b\cdot b=240\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\cdot b\\\dfrac{5}{3}\cdot b^2=240\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\cdot b\\b^2=240:\dfrac{5}{3}=240\cdot\dfrac{3}{5}=144\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\cdot b\\\left[{}\begin{matrix}b=12\left(nhận\right)\\b=-12\left(loại\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\cdot12=20\\b=12\end{matrix}\right.\)(thỏa ĐK)
Chu vi hình chữ nhật là:
\(C=2\cdot\left(a+b\right)=2\cdot\left(12+20\right)=64\left(m\right)\)
Vậy: Chu vi hình chữ nhật là 64m

Gọi chiều rộng là x
Chiều dài là 17,5-x
Theo đề, ta có: \(\left(20,5-x\right)\left(x+2\right)=x\left(17,5-x\right)+45\)
\(\Leftrightarrow20,5x+41-x^2-2x=17,5x-x^2+45\)
=>18,5x+41=17,5x+45
=>x=4
Vậy: Chiều rộng là 4m
Chiều dài là 13,5m

Câu 1:
Gọi chiều rộng khu vườn là \(x\) (m) \(\left(x>0\right)\)
\(\Rightarrow\) Chiều dài khu vườn là \(\dfrac{7}{4}x\) (m).
Diện tích khu vườn là 1792 m2 \(\Rightarrow\dfrac{7}{4}x^2=1792\)
\(\Rightarrow x^2=1024\Rightarrow x=32\) (m)
\(\Rightarrow\) Chiều rộng khu vườn là \(32\)m, chiều dài khu vườn là \(\dfrac{7}{4}.32=56\)m
\(\Rightarrow\) Chu vi khu vườn là: \(2.\left(32+56\right)=176\) (m).
(Bạn có thể gọi chiều dài là x, chiều rộng là y nhé.)
Câu 2:
Bạn kiểm tra lại đề bài nhé. Thiếu dữ kiện để có thể lập được hệ phương trình ạ.
Câu 2:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của mảnh vườn(Điều kiện: a>0; b>0 và \(a\ge b\))
Vì diện tích ban đầu của mảnh vườn là 720m2 nên ta có phương trình:
ab=720(1)
Vì khi tăng chiều dài 6m và giảm chiều rộng 4m thì diện tích mảnh vườn không đổi nên ta có phương trình:
\(\left(a+6\right)\left(b-4\right)=720\)
\(\Leftrightarrow ab-4a+6b-24=720\)
\(\Leftrightarrow-4a+6b-24=0\)
\(\Leftrightarrow-4a+6b=24\)(2)
Từ (1) và (2) ta có được hệ phương trình:
\(\left\{{}\begin{matrix}ab=720\\-4a+6b=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\-4\cdot\dfrac{720}{b}+6b=24\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\-\dfrac{2880}{b}+6b=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\6b^2-24b-2880=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\6\left(b^2-4b-480\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\b^2-4b+4-484=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\\left(b-2\right)^2-484=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\\left(b-2-22\right)\left(b-2+22\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\\left(b-24\right)\left(b+20\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\\left[{}\begin{matrix}b-24=0\\b+20=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{b}\\\left[{}\begin{matrix}b=24\left(nhận\right)\\b=-20\left(loại\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{720}{24}=30\left(nhận\right)\\b=24\end{matrix}\right.\)
Vậy: Chiều dài của mảnh vườn là 30m; Chiều rộng của mảnh vườn là 24m

Đáp án B
Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)
Chiều dài hình chữ nhật lúc đầu: 3x (cm)
Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)
Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)
Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153
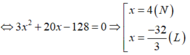
Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm
Suy ra chu vi hình chữ nhật ban đầu là: (12 + 4).2 = 32 (cm)

Đáp án B
Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)
Chiều dài hình chữ nhật lúc đầu: 3x (cm)
Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)
Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)
Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153
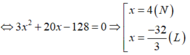
Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm
Suy ra chu vi hình chữ nhật ban đầu là: (12 + 4).2 = 32 (cm)

Gọi chiều rộng của HCN là x cm ( x > 0)
-> Chiều dài hcn là 2x cm
Biết diện tích HCN là 98 cm
ta có pt x.2x= 98 <=> 2x2 =98 <=> x2 = 46 <=> x= 8cm
Vậy chiều rộng HCN là 8cm
Và chiều dài hcn là 2.8=16cm
-> Chu vi HCN là .....
