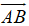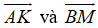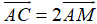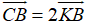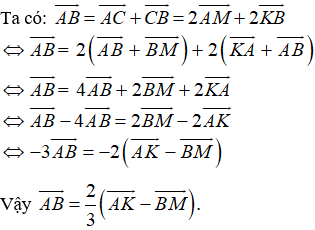Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M là trung điểm của AC nên
K là trung điểm của BC nên
Bạn tự vẽ hình minh họa nha :>
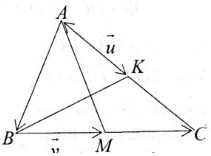
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có 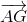 =
= 
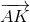 =>
=> 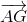 =
=

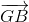 = -
= -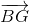 = -
= -
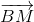 = -
= -

Theo quy tắc 3 điểm đối với tổng vec-tơ:
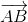 =
= 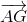 +
+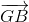 =>
=> 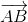 =
= 
 -
- 
 =
=  (
( -
-  ).
).
AK là trung tuyến thuộc cạnh BC nên
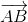 +
+ 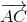 = 2
= 2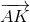 =>
=> 
 -
- 
 +
+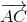 = 2
= 2
Từ đây ta có 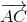 =
= 
 +
+
 =>
=> 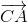 = -
= -
 -
- 
 .
.
BM là trung tuyến thuộc đỉnh B nên:
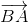 +
+ 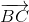 = 2
= 2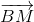 => -
=> - 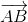 +
+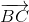 = 2
= 2
=> 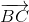 =
= 
 +
+
 .
.

a: \(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)

Lời giải:
Ta có:
\(\overrightarrow{AB}=\overrightarrow{AM}+\overrightarrow{MB}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}=\overrightarrow{AM}-\overrightarrow{BN}+\overrightarrow{MN}\)
Vì $AM,BN$ là trung tuyến nên $M,N$ lần lượt là trung điểm của $BC, AC$
$\Rightarrow MN$ là đường trung bình của tam giác $ABC$ ứng với $AB$
\(\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BA}=-\frac{1}{2}\overrightarrow{AB}\). Do đó:
\(\overrightarrow{AB}=\overrightarrow{AM}-\overrightarrow{BN}-\frac{1}{2}\overrightarrow{AB}\Leftrightarrow \frac{3}{2}\overrightarrow{AB}=\overrightarrow{AM}-\overrightarrow{BN}\)
\(\Leftrightarrow \overrightarrow{AB}=\frac{2}{3}\overrightarrow{AM}-\frac{2}{3}\overrightarrow{BN}\)
Cho tam giác ABC có trung tuyến BM và trọng tâm G . Phân tích vecto BG theo hai vecto BA và vecto BC

\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\)

\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=-\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)

Câu 1:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)