Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp 1: k = 1 và O ∈ a thì A’B’ = AB hay a = a’.
- Trường hợp 2: k ≠ 1 và O ∉ a thì A’B’ // AB hay a’ // a
Vậy qua V(0,k) biến mp (α) thành mp(α') = mp(α).
- Nếu O ∈ mp(α) và k ≠ 1. Trên mp(α) lấy hai đường thẳng a, b cắt nhau tại I.
Qua phép vị tự tâm O tỉ số k :
+ Biến hai đường thẳng a, b thành 2 đường thẳng a’, b’ song song hoặc trùng với a,b
+ Biến giao điểm I thành điểm I’ là giao điểm của hai đường thẳng a’ và b’
HT

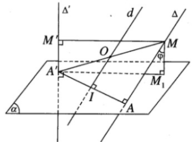
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

Ta có: a ∆ → = (2; 3; 2) và n α → = (2; −2; 1)
a ∆ → . n α → = 4 – 6 + 2 = 0 (1)
Xét điểm M 0 (-3; -1; -1) thuộc ∆ , ta thấy tọa độ M 0 không thỏa mãn phương trình của ( α ) . Vậy M 0 ∉ ( α ) (2).
Từ (1) và (2) ta suy ra ∆ // ( α ).

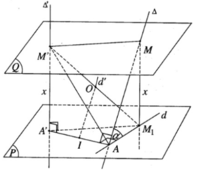
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.