Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

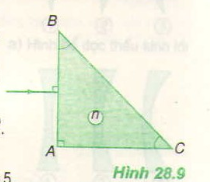
Cho một lăng kính có chiết suất 1,5 đặt trong không khí, tiết diện thẳng là một tam giác ABC, có góc A = 75° và góc B = 60°. Trong mặt phẳng ABC, chiếu tới trung điểm của AB một chùm sáng hẹp, song song với góc tới 32°. Tia ló ra khỏi lăng kính lệch so với tia tới một góc gần giá trị nào nhất sau đây?
A. 30°.
B. 75°.
C. 78°.
D. 90°.

Bài 8:
a, F = 0,18N
b, Để lực tăng 4 lần thì khoảng cách giảm 2 lần -> khoảng cách là 3/2=1,5 cm
c)k/c giữa 2 điện tích là 1,5cm
Bài 9
a)2,67.10^−9 C
b)1,6cm.
Giải thích các bước giải:
Gọi độ lớn hai điện tích là q.
a) Lực tương tác giữa hai điện tích khi chúng cách nhau đoạn r1 là:
F1 = k q2/r1^2 ⇒ 1,6.10^−4 = 9.10^9. q2/0,02^2 ⇒ q=2,67.10^−9 (C)
b) Lực tương tác giữa hai điện tích khi khoảng cách giữa chúng là r2 là:
F2 = k q2/r2^2 ⇒ 2,5.10^−4 = 9.10^9.(2,67.10−9)^2/r2^2 ⇒ r2 = 0,016 (m) = 1,6 (cm)

Bài 8 :
Đáp án:
a) F= 0,18 N
b)k/c giữa chúng giảm 2 lần
.Bài 9:
Đáp án:
a) độ lớn 2 đh =2,67.10-9 C
b)r2=1,6cm
\(\left\{{}\begin{matrix}sin\left(i_{gh}\right)=\dfrac{1}{n}\xrightarrow[]{n=1,5}i_{gh}=41,81^o\\sin\left(i_1\right)=n.sin\left(r_1\right)\xrightarrow[i_1=17^o]{n=1,5}r_1=11,239^o\\r_1+r_2=A\xrightarrow[]{A=60^o}r_2=48,761^o>i_{gh}\\r_2+r_3=C\xrightarrow[]{C=60^o}11,239^o=r_1\end{matrix}\right.\)
\(n.sin\left(r_3\right)=sin\left(i_3\right)\Rightarrow i_3=17^o\)
Tia IJ quay theo chiều kim đồng hồ với góc SI một góc là:
\(D_1=17^o-11,239^o=5,761^o\)
Tia JK quay theo chiều kìm đồng hồ so với góc IJ một góc là:
\(D_2=180^o-2.48.761^o=82,478^o\)
Tia KR quay theo chiều kim đồng hồ so với góc JK là:
\(D_3=17^o-11,239^o=5,761^o\)
Vậy tia ló lệch tia tới:
\(D_1+D_2+D_3=94^o\)
⇒ Chọn A