Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

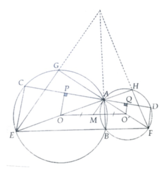
Vẽ OP ⊥ CA; O’Q ⊥ AD suy ra tứ giác OPQO’ là hình thang vuông tại P, Q
a, Kẻ OP; O’Q ⊥ CD do CD ⊥ MA và M là trung điểm của OO’ => AP=AQ => AC=AD
b,i, Chú ý ∆EAF có AB, EG,FI là ba đường cao
ii, Sử dụng CD= 2PQ để lập luận, ta có
Kết luận: CD lớn nhất khi CD//OO’

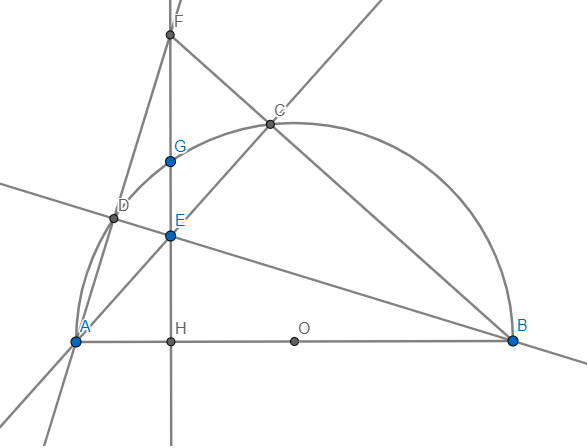
a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm
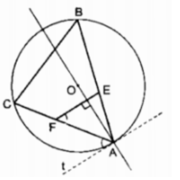

a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>BE\(\perp\)AM
Xét (O) có
ΔAFB nội tiếp
AB là đường kính
Do đó: ΔAFB vuông tại F
=>BF\(\perp\)AN
Xét ΔABM vuông tại B có BE là đường cao
nên \(AE\cdot MA=AB^2\left(1\right)\)
Xét ΔABN vuông tại B có BF là đường cao
nên \(AF\cdot AN=AB^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AM=AF\cdot AN\)